Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.





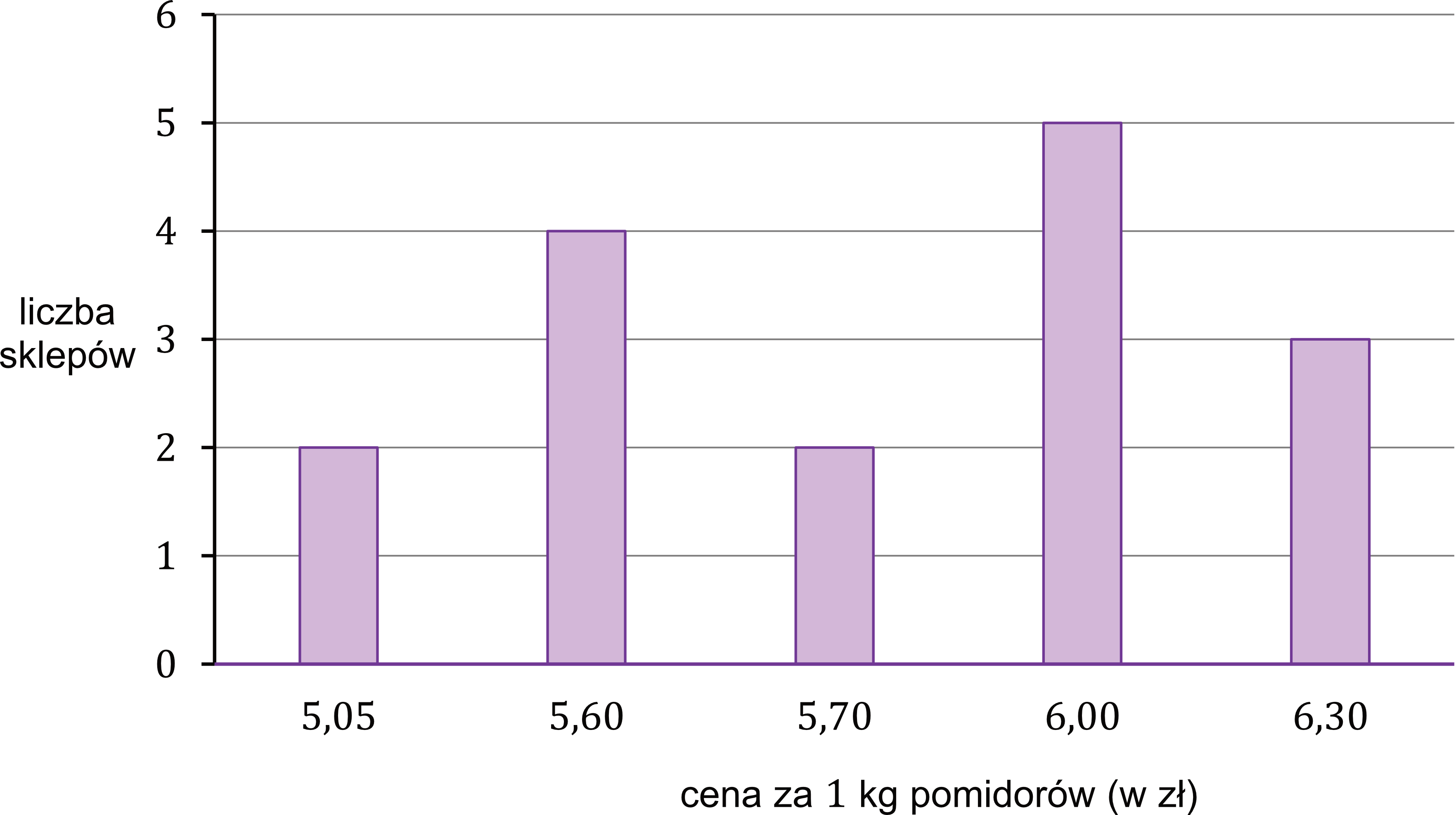
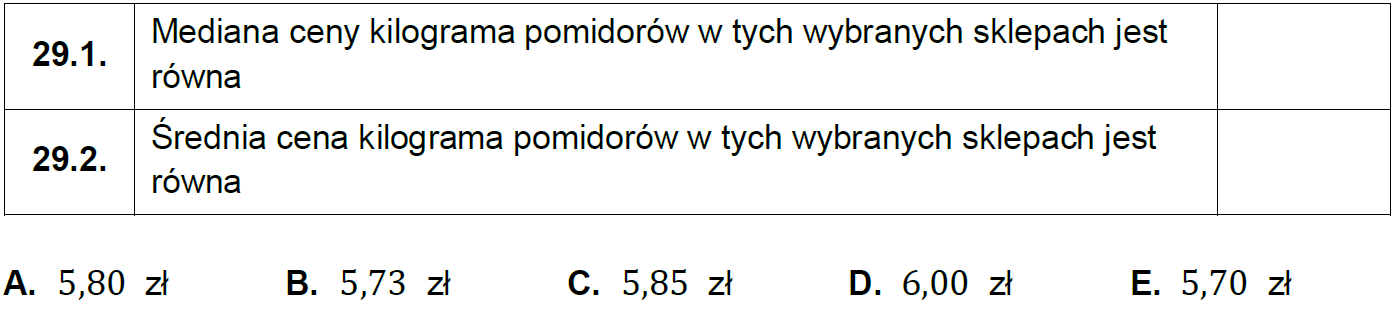
Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.

Odpowiedź:      

C oraz A

Rozwiązanie:      
Krok 1. Obliczenie mediany ceny kilograma pomidorów. Zebrano ceny pomidorów z \(16\) sklepów, czyli liczba wyników jest parzysta. To oznacza, że mediana będzie średnią arytmetyczną między środkowymi wyrazami - czyli w naszym przypadku będzie to średnia arytmetyczna ósmego i dziewiątego wyniku. Wyliczając medianę musimy uporządkować liczby w porządku niemalejącym (czyli od najmniejszych do największych). Jeśli chcemy, to moglibyśmy wypisać te ceny jako ciąg: $$5,05; \; 5,05; \; 5,60; \; 5,60...$$ Analizując wykres i pojawiające się tam ceny wynika, że ósmą w kolejności ceną byłoby \(5,70\), a dziewiątą byłoby już \(6,00\). To oznacza, że mediana będzie równa: $$m=\frac{5,70+6,00}{2} \           ,\ m=\frac{11,70}{2} \           ,\ m=5,85$$ Krok 2. Obliczenie średniej ceny kilograma pomidorów. Średnią cenę obliczymy w następujący sposób: $$śr=\frac{2\cdot5,05+4\cdot5,60+2\cdot5,70+5\cdot6,00+3\cdot6,30}{16} \           ,\ śr=\frac{10,10+22,40+11,40+30+18,90}{16} \           ,\ śr=\frac{92,80}{16} \           ,\ śr=5,80$$

Teoria:      
W trakcie opracowania