Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem \(30°\) i ma długość równą \(6\) (zobacz rysunek).





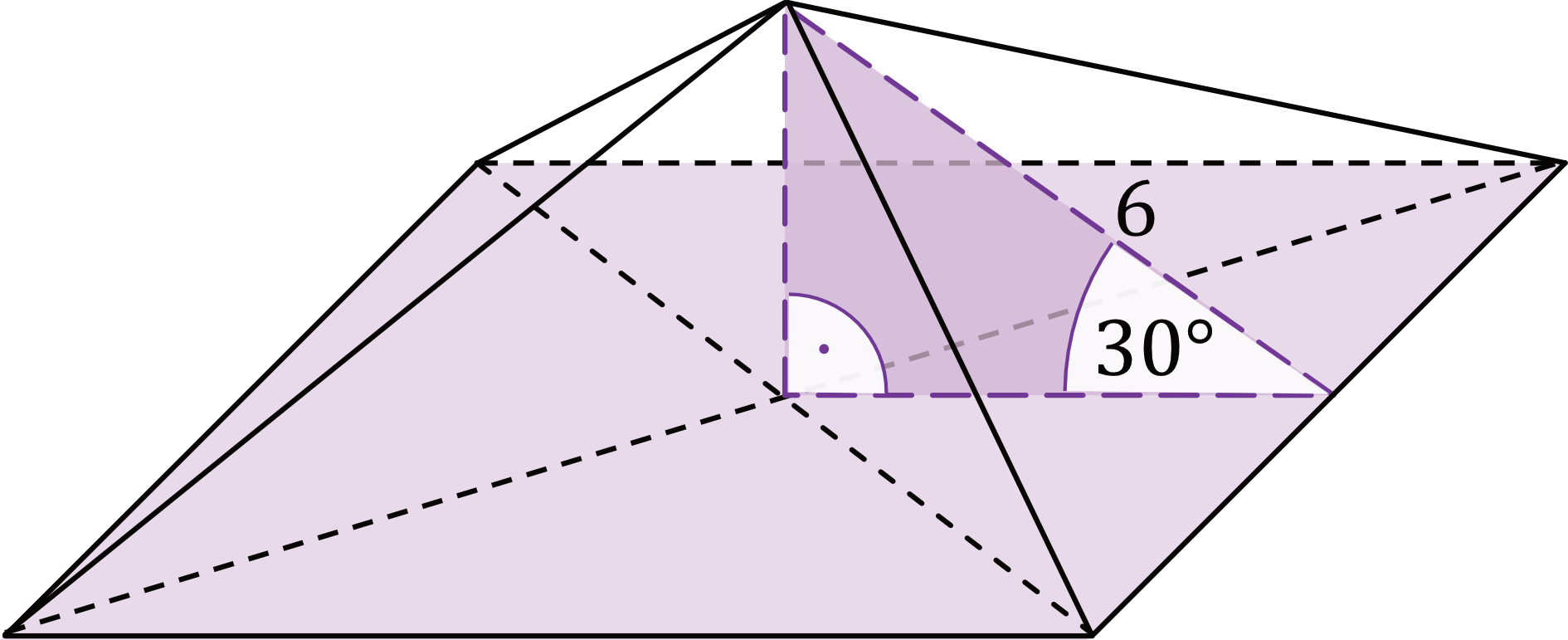
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Zapisz obliczenia.

Odpowiedź:      

\(V=108\) oraz \(P_{c}=108+72\sqrt{3}\)

Rozwiązanie:      
Krok 1. Obliczenie wysokości ostrosłupa. Spójrzmy na trójkąt prostokątny, który został narysowany w treści zadania. Jest to klasyczny trójkąt o kątach \(30°, 60°, 90°\). Z własności tego trójkąta wynika, że krótsza przyprostokątna (którą w tym przypadku jest wysokość ostrosłupa) będzie dwa razy krótsza od przeciwprostokątnej. Tym samym możemy zapisać, że: $$H=6:2 \           ,\ H=3$$ Do tego samego wyniku dojdziemy korzystając z funkcji trygonometrycznej - w tej sytuacji sprawdzi się sinus: $$sin30°=\frac{H}{6} \           ,\ \frac{1}{2}=\frac{H}{6} \           ,\ H=3$$ Krok 2. Obliczenie długości krawędzi podstawy. Spójrzmy jeszcze raz na nasz trójkąt o kątach \(30°, 60°, 90°\). Z własności tego trójkąta wynika to, że jego dolna (dłuższa) przyprostokątna będzie \(\sqrt{3}\) razy dłuższa od krótszej przyprostokątnej, czyli moglibyśmy zapisać, że ta dolna przyprostokątna ma długość \(x=3\sqrt{3}\). W podstawie ostrosłupa znajduje się kwadrat (wiemy to, ponieważ ostrosłup jest prawidłowy czworokątny). Ta dolna przyprostokątna naszego analizowanego przed chwilą trójkąta będzie więc połową długości boku kwadratu. To oznacza, że w takim razie: $$a=2\cdot3\sqrt{3} \           ,\ a=6\sqrt{3}$$ Krok 3. Obliczenie pola podstawy oraz pola powierzchni bocznej. W podstawie naszej bryły mamy kwadrat o boku \(a=6\sqrt{3}\), zatem pole powierzchni podstawy będzie równe: $$P_{p}=(6\sqrt{3})^2 \           ,\ P_{p}=36\cdot3 \           ,\ P_{p}=108$$ Ściany boczne naszej bryły to trójkąty o podstawie \(a=6\sqrt{3}\) oraz wysokości \(h=6\). Mamy cztery takie ściany, więc pole powierzchni bocznej będzie równe: $$P_{b}=4\cdot\frac{1}{2}\cdot6\sqrt{3}\cdot6 \           ,\ P_{b}=72\sqrt{3}$$ Krok 4. Obliczenie objętości ostrosłupa. Znając pole podstawy oraz wysokość ostrosłupa, możemy zapisać, że: $$V=\frac{1}{3}\cdot P_{p}\cdot H \           ,\ V=\frac{1}{3}\cdot108\cdot3 \           ,\ V=108$$ Krok 5. Obliczenie pola powierzchni całkowitej. Znając pole podstawy oraz pole powierzchni bocznej, możemy zapisać, że: $$P_{c}=P_{p}+P_{b} \           ,\ P_{c}=108+72\sqrt{3}$$

Teoria:      
W trakcie opracowania