Dany jest sześcian \(ABCDEFGH\). Przekątne \(AC\) i \(BD\) ściany \(ABCD\) sześcianu przecinają się w punkcie \(P\) (zobacz rysunek).





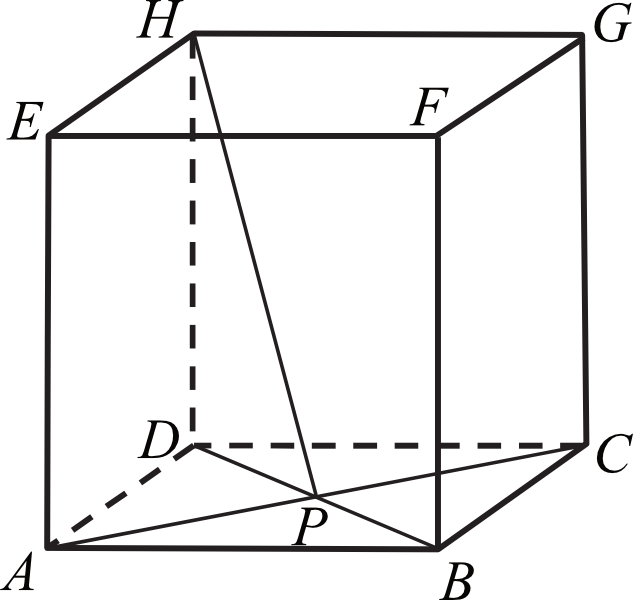
Tangens kąta, jaki odcinek \(PH\) tworzy z płaszczyzną \(ABCD\), jest równy:

A \(\frac{\sqrt{2}}{2}\)
B \(\frac{1}{2}\)
C \(1\)
D \(\sqrt{2}\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. W sześcianie wszystkie krawędzie mają jednakową długość, oznaczmy ją jako \(a\). Dodatkowo zaznaczmy interesujący nas kąt, czyli kąt między odcinkiem \(PH\) i płaszczyzną podstawy: Aby obliczyć wartość tangensa naszego kąta będziemy potrzebować długości dwóch przyprostokątnych trójkąta \(DPH\). Wiemy już, że \(|DH|=a\), musimy jeszcze wyznaczyć długość odcinka \(DP\). Krok 2. Obliczenie długości odcinka \(DP\). Odcinek \(DP\) to połowa przekątnej kwadratu znajdującego się w podstawie. Skoro w podstawie mamy kwadrat o boku \(a\), to jego cała przekątna ma długość \(a\sqrt{2}\). Nasz odcinek \(DP\) jest połową tej długości, czyli: $$|DP|=\frac{1}{2}a\sqrt{2}=\frac{a\sqrt{2}}{2}$$ Krok 3. Obliczenie wartości tangensa. Znamy długości dwóch przyprostokątnych, więc jesteśmy w stanie wyznaczyć poszukiwaną wartość tangensa naszego kąta: $$tgα=\frac{|DH|}{|DP|} \           ,\ tgα=\frac{a}{\frac{a\sqrt{2}}{2}} \           ,\ tgα=a:\frac{a\sqrt{2}}{2} \           ,\ tgα=a\cdot\frac{2}{a\sqrt{2}} \           ,\ tgα=\frac{2}{\sqrt{2}}$$ Usuwając niewymierność z mianownika otrzymamy: $$tgα=\frac{2}{\sqrt{2}} \           ,\ tgα=\frac{2\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}} \           ,\ tgα=\frac{2\sqrt{2}}{2}=\sqrt{2}$$

Teoria:      
W trakcie opracowania