Na rysunku przedstawiono bryłę zbudowaną z walca i półkuli. Wysokość walca jest równa \(r\) i jest taka sama jak promień półkuli oraz taka sama jak promień podstawy walca.





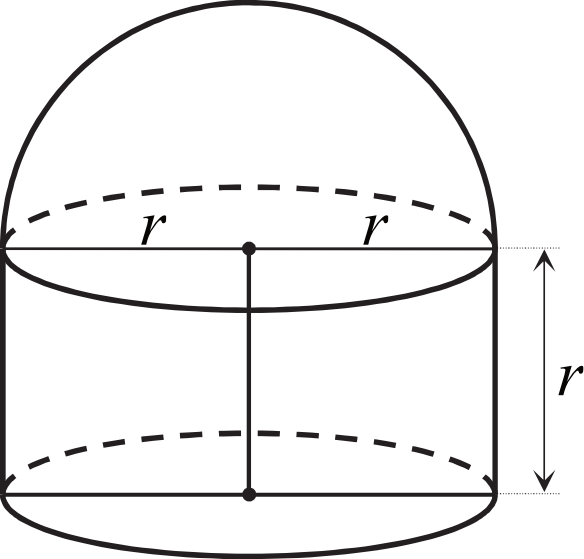
Objętość tej bryły jest równa:

A \(\frac{5}{3}πr^3\)
B \(\frac{4}{3}πr^3\)
C \(\frac{2}{3}πr^3\)
D \(\frac{1}{3}πr^3\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Obliczenie objętości walca. Nasza bryła składa się z walca i półkuli, zatem aby obliczyć jej objętość musimy obliczyć oddzielnie objętość jednej i drugiej części. Zaczynając od walca możemy zauważyć, że w tym przypadku wysokość walca jest równa \(r\), zatem: $$V_{w}=P_{p}\cdot h \           ,\ V_{w}=πr^2\cdot r \           ,\ V_{w}=πr^3$$ Krok 2. Obliczenie objętości kuli. Objętość kuli wyraża się wzorem \(V=\frac{4}{3}πr^3\). W naszym zadaniu mamy jednak półkulę, więc połowę kuli. To oznacza, że całość będziemy musieli jeszcze przemnożyć przez \(\frac{1}{2}\). $$V_{p}=\frac{1}{2}\cdot\frac{4}{3}πr^3 \           ,\ V_{p}=\frac{2}{3}πr^3$$ Krok 3. Obliczenie objętości całej bryły. Objętość całej bryły jest sumą objętości walca i półkuli, zatem: $$V=V_{w}+V_{p} \           ,\ V=πr^3+\frac{2}{3}πr^3 \           ,\ V=\frac{5}{3}πr^3$$

Teoria:      
W trakcie opracowania