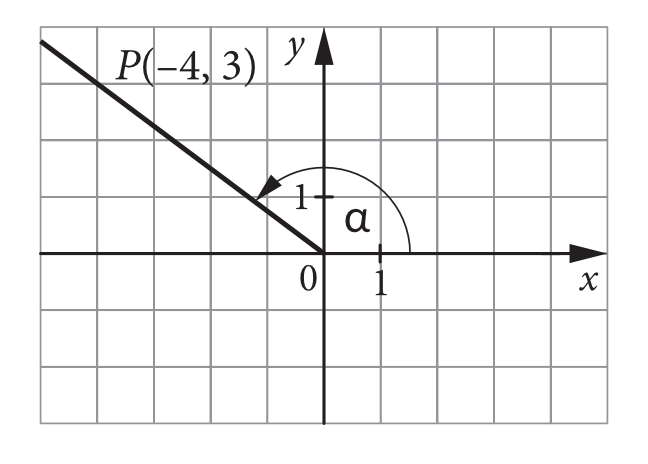
Wskaż poprawną wartość funkcji trygonometrycznej kąta rozwartego \(α\) (rysunek obok).

A \(cosα=-\frac{4}{5}\)
B \(cosα=\frac{4}{5}\)
C \(sinα=\frac{3}{4}\)
D \(tgα=-\frac{4}{3}\)

Odpowiedź:      

A

Rozwiązanie:      
Z tablic matematycznych możemy odczytać, że jeżeli mamy taką sytuację jak na powyższym rysunku, czyli kiedy jedno ramię kąta pokrywa się z osią iksów, wierzchołek kąta znajduje się w miejscu przecięcia się osi układu współrzędnych, a drugie ramię przechodzi przez punkt \(P=(x;y)\), to: $$sinα=\frac{y}{r} \           ,\ cosα=\frac{x}{r} \           ,\ tgα=\frac{y}{x}$$ gdzie \(r\) to odległość od punktu \(P\) do początku układu współrzędnych, którą możemy policzyć ze wzoru \(r=\sqrt{x^2+y^2}\). Krok 2. Obliczenie długości \(r\). W naszym przypadku ramię kąta przechodzi przez punkt \(P=(-4;3)\), czyli \(x=-4\) oraz \(y=3\). Korzystając z podanego powyżej wzoru możemy zapisać, że: $$r=\sqrt{x^2+y^2} \           ,\ r=\sqrt{(-4)^2+3^2} \           ,\ r=\sqrt{16+9} \           ,\ r=\sqrt{25} \           ,\ r=5$$ Krok 3. Obliczenie wartości poszczególnych funkcji trygonometrycznych. Wiemy już, że \(x=-4\), \(y=3\) oraz \(r=5\), zatem możemy obliczyć każdą z wartości funkcji trygonometrycznych: $$sinα=\frac{3}{5} \           ,\ cosα=\frac{-4}{5}=-\frac{4}{5} \           ,\ tgα=\frac{3}{-4}=-\frac{3}{4}$$ Porównując otrzymane wyniki z odpowiedziami widzimy wyraźnie, że prawidłowa jest pierwsza odpowiedź.

Teoria:      
W trakcie opracowania