Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura próbna z matematyki (poziom podstawowy) - Nowa Era 2015 Zadanie 17 z 33
Zadanie nr 17. (1pkt)
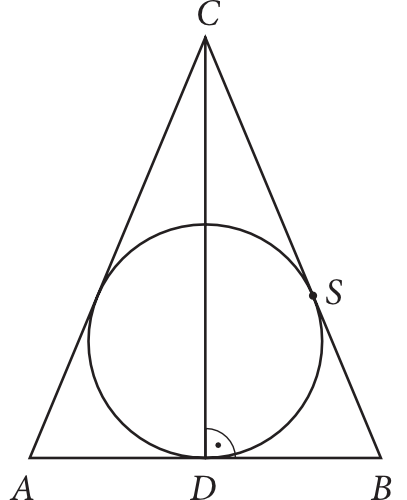
W trójkąt równoramienny \(ABC\) o podstawie \(AB\) wpisano okrąg o promieniu \(5\). Odległość wierzchołka \(C\) od punktu styczności \(S\) okręgu z ramieniem \(BC\) jest równa \(12\). Wysokość \(CD\) tego trójkąta ma długość:
A \(10\)
B \(15\)
C \(5+\sqrt{119}\)
D \(18\)
Rozwiązanie:
Krok 1. Sporządzenie rysunku pomocniczego.
Nanosząc na rysunek odpowiednie informacje z treści zadania oraz łącząc środek okręgu z punktem styczności \(S\) otrzymamy następującą sytuację:
Krok 2. Obliczenie długości odcinka \(CO\).
Spójrzmy na trójkąt prostokątny \(OSC\). Korzystając z Twierdzenia Pitagorasa możemy zapisać, że:
$$|OS|^2+|SC|^2=|CO|^2 \ ,\
5^2+12^2=|CO|^2 \ ,\
25+144=|CO|^2 \ ,\
|CO|^2=169 \ ,\
|CO|=13 \quad\lor\quad |CO|=-13$$
Długość odcinka nie może być ujemna, zatem zostaje nam jedynie \(|CO|=13\).
Krok 3. Obliczenie wysokości \(CD\).
Patrząc się na rysunek możemy teraz zauważyć, że wysokość trójkąta będzie równa sumie długości odcinka \(CO\) (którą obliczyliśmy przed chwilą) oraz \(OD\) (który jest równy długości promienia okręgu), zatem:
$$|CD|=13+5 \ ,\
|CD|=18$$
Teoria:
W trakcie opracowania
matura próbna - Nowa Era

