Na rysunku przedstawiono interpretację geometryczną jednego z niżej zapisanych układów równań.





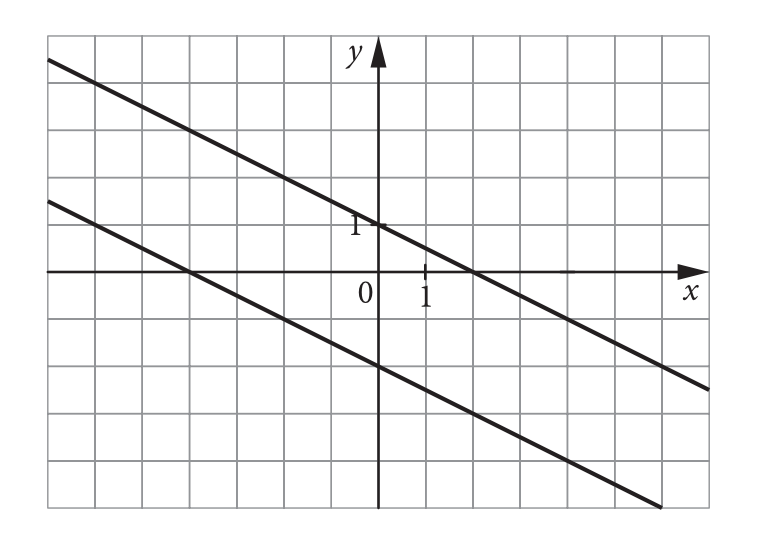
Wskaż ten układ:

A \(\begin{cases}
y=-\frac{1}{2}x-2 \           ,\
y=-\frac{1}{2}x+1
\end{cases}\)
B \(\begin{cases}
y=\frac{1}{2}x-2 \           ,\
y=\frac{1}{2}x+1
\end{cases}\)
C \(\begin{cases}
y=-\frac{1}{2}x+2 \           ,\
y=-\frac{1}{2}x-1
\end{cases}\)
D \(\begin{cases}
y=-2x-2 \           ,\
y=2x+1
\end{cases}\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Odczytanie z rysunku kluczowych informacji na temat prostych. Z rysunku wynika, że obydwie proste są malejące, czyli na pewno muszą mieć współczynnik kierunkowy \(a\) mniejszy od \(0\). Oprócz tego jesteśmy też w stanie odczytać konkretne wartości współczynnika \(b\), patrząc się na miejsce przecięcia się prostych z osią igreków. Jedna prosta przecina oś igreków dla \(y=1\), czyli współczynnik \(b=1\), natomiast druga prosta przecina oś igreków dla \(y=-2\), czyli ma współczynnik \(b=-2\). Krok 2. Wskazanie prawidłowego układu równań. Proste zapisane w układach równań mają postać \(y=ax+b\). Ustaliliśmy już sobie, że współczynnik \(a\) jednej i drugiej prostej musi być ujemny, co sprawia że możemy odrzucić drugą i czwartą odpowiedź. Wiemy też, że współczynnik \(b\) jednej prostej ma być równy \(1\), a drugiej ma być równy \(-2\) i taką sytuację mamy w pierwszym układzie równań. Możemy więc bez wykonywania specjalnych obliczeń wskazać, że poszukiwaną prawidłową odpowiedzią jest pierwszy układ równań.

Teoria:      
W trakcie opracowania