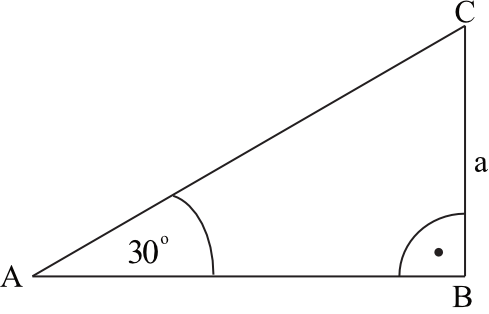
Obwód trójkąta przedstawionego na rysunku jest równy:

A \(\left(3+\frac{\sqrt{3}}{2}\right)a\)
B \(\left(2+\frac{\sqrt{2}}{2}\right)a\)
C \((3+\sqrt{3})a\)
D \((2+\sqrt{2})a\)

Odpowiedź:      

C

Rozwiązanie:      
W tym zadaniu najprościej będzie wykorzystać własności trójkątów \(30°, 60°, 90°\). Z tych własności wynika wprost, że długość dłuższej przyprostokątnej jest równa \(|AB|=a\sqrt{3}\), a długość przeciwprostokątnej wynosi \(|AC|=2a\). Obwód trójkąta będzie więc równy: $$Obw=a+a\sqrt{3}+2a \           ,\ Obw=3a+a\sqrt{3} \           ,\ Obw=(3+\sqrt{3})a$$ Gdybyśmy o tych własnościach nie pamiętali, to do wyznaczenia długości boków zawsze możemy posłużyć się jeszcze funkcjami trygonometrycznymi: Wyznaczenie długości boku \(AB\): $$tg30°=\frac{a}{|AB|} \           ,\ \frac{\sqrt{3}}{3}=\frac{a}{|AB|} \quad\bigg/\cdot |AB| \           ,\ a=\frac{\sqrt{3}}{3}|AB| \quad\bigg/\cdot\frac{3}{\sqrt{3}} \           ,\ |AB|=\frac{3}{\sqrt{3}}a \           ,\ |AB|=\frac{3\sqrt{3}}{3}a \           ,\ |AB|=a\sqrt{3}$$ Wyznaczenie długości boku \(AC\): $$sin30°=\frac{a}{|AC|} \           ,\ \frac{1}{2}=\frac{a}{|AC|} \quad\bigg/\cdot |AC| \           ,\ a=\frac{1}{2}|AC| \quad\bigg/\cdot2 \           ,\ |AC|=2a$$

Teoria:      
W trakcie opracowania