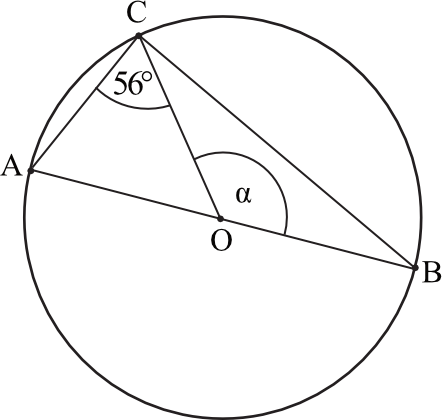
Na okręgu o środku w punkcie \(O\) leży punkt \(C\) (zobacz rysunek). Odcinek \(AB\) jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy \(α\) ma miarę:

A \(116°\)
B \(114°\)
C \(112°\)
D \(110°\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Wyznaczenie miary kąta \(CAO\). Trójkąt \(AOC\) jest na pewno równoramienny, a jego ramionami są boki \(AO\) oraz \(CO\). Skąd to wiemy? Obydwa te boki są długością promienia naszego okręgu. To z kolei oznacza, że kąty przy podstawie \(AC\) mają równą miarę, zatem: $$|\sphericalangle CAO|=|\sphericalangle ACO|=56°$$ Krok 2. Obliczenie miary kąta \(COB\), czyli kąta \(α\). Obliczony przed chwilą kąt \(CAO\) oraz nasz kąt \(α\) są oparte na tym samym łuku \(CB\). W związku z tym miara kąta środkowego będzie dwa razy większa od miary kąta wpisanego. Zatem: $$α=56°\cdot2=112°$$

Teoria:      
W trakcie opracowania