Na rysunku przedstawiono fragment wykresu funkcji wykładniczej \(f\) określonej wzorem \(f(x)=a^x\). Punkt \(A=(1,2)\) należy do wykresu funkcji.







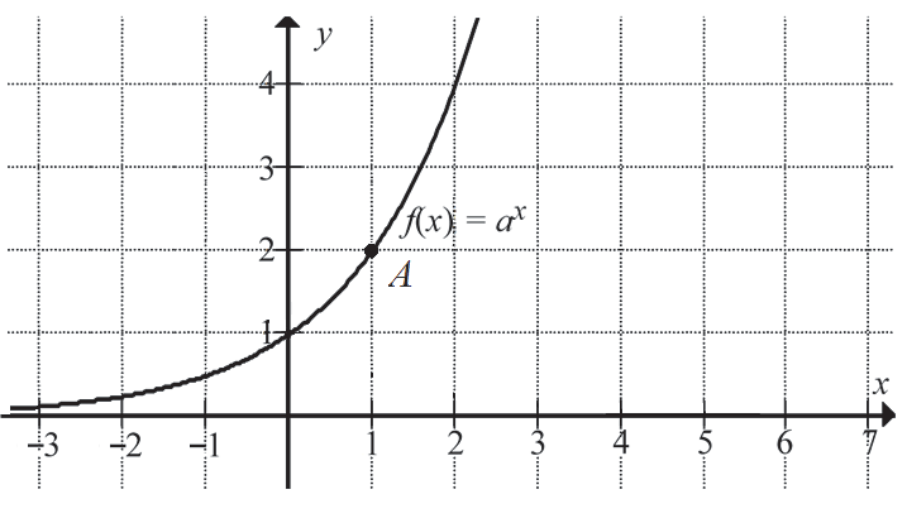
Podstawa \(a\) potęgi jest równa:

A \(-\frac{1}{2}\)
B \(\frac{1}{2}\)
C \(-2\)
D \(2\)

Odpowiedź:      

D

Rozwiązanie:      
Wykres funkcji możemy zapisać jako \(y=a^x\). Teraz znacznie lepiej widać, że możemy do wzoru tej funkcji po prostu podstawić współrzędne punktu \(A=(1,2)\) i tym samym wyznaczyć podstawę potęgi, zatem: $$y=a^x \           ,\ 2=a^1$$ No i teraz musimy sobie odpowiedzieć na pytanie - jaką liczbę trzeba podnieść do potęgi pierwszej aby otrzymać \(2\)? Oczywiście \(2\), tak więc prawidłową odpowiedzią będzie \(a=2\).

Teoria:      
W trakcie opracowania