W trójkącie \(ABC\) punkt \(D\) leży na boku \(BC\), a punkt \(E\) leży na boku \(AB\). Odcinek \(DE\) jest równoległy do boku \(AC\), a ponadto \(|BD|=10\), \(|BC|=12\) i \(|AC|=24\) (zobacz rysunek).







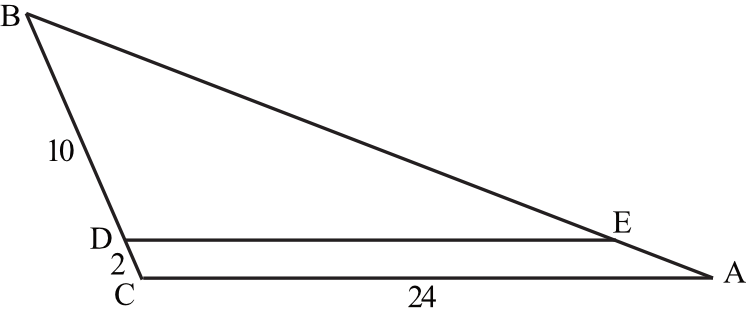
Długość odcinka \(DE\) jest równa:

A \(22\)
B \(20\)
C \(12\)
D \(11\)

Odpowiedź:      

B

Rozwiązanie:      
Skoro odcinek \(DE\) jest równoległy do boku \(CA\), to trójkąty \(ABC\) oraz \(EBD\) są trójkątami podobnymi (na mocy cechy kąt-kąt-kąt). Stosunek boków odpowiadających sobie będzie taki sam, co pozwoli ułożyć nam następujące równanie: $$\frac{|DE|}{|CA|}=\frac{|BD|}{|BC|} \           ,\ \frac{|DE|}{24}=\frac{10}{10+2} \           ,\ \frac{|DE|}{24}=\frac{10}{12} \quad\bigg/\cdot24 \           ,\ |DE|=\frac{240}{12} \           ,\ |DE|=20$$

Teoria:      
W trakcie opracowania