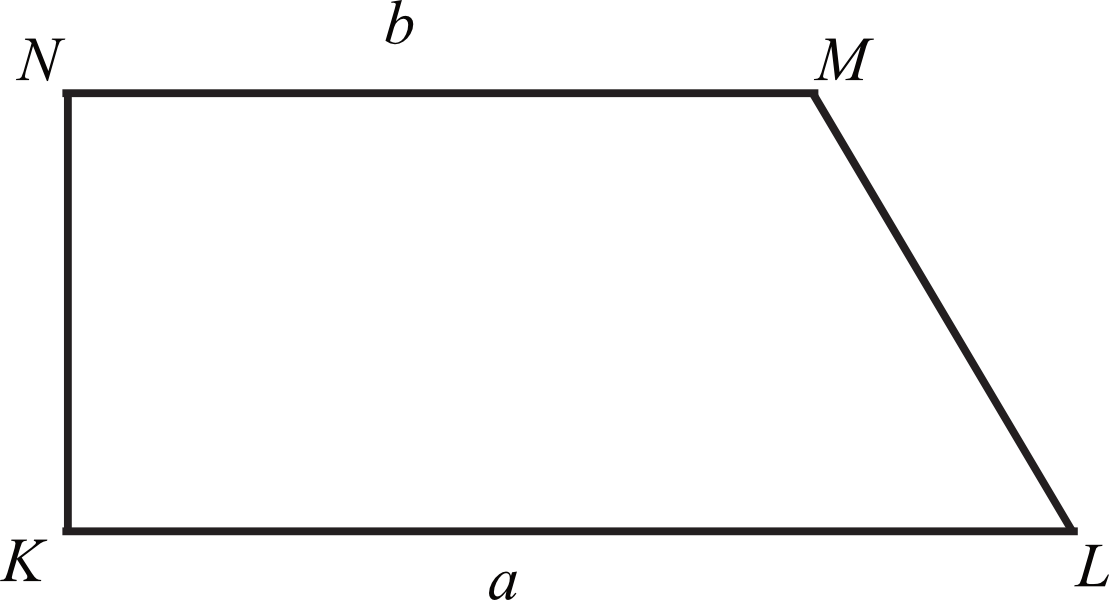
Dany jest trapez prostokątny \(KLMN\), którego podstawy mają długości \(|KL|=a\), \(|MN|=b\), \(a\gt b\). Kąt \(KLM\) ma miarę \(60°\). Długość ramienia \(LM\) tego trapezu jest równa:

A \(a-b\)
B \(2(a-b)\)
C \(a+\frac{1}{2}b\)
D \(\frac{a+b}{2}\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Dorysowując do naszego trapezu wysokość otrzymamy następujący szkic: Krok 2. Obliczenie długości ramienia \(LM\). Spójrzmy na powstały trójkąt prostokątny \(PLM\). Znamy miarę kąta ostrego leżącego przy przyprostokątnej \(LM\). Szukamy długości przeciwprostokątnej, zatem korzystając z cosinusa zapiszemy: $$cos60°=\frac{a-b}{x} \           ,\ \frac{1}{2}=\frac{a-b}{x} \quad\bigg/\cdot x \           ,\ \frac{1}{2}x=a-b \quad\bigg/\cdot2 \           ,\ x=2\cdot(a-b)$$

Teoria:      
W trakcie opracowania