W trójkącie \(ABC\), w którym \(|AC|=|BC|\), na boku \(AB\) wybrano punkt \(D\) taki, że \(|BD|=|CD|\) oraz \(|\sphericalangle ACD|=21°\) (zobacz rysunek).







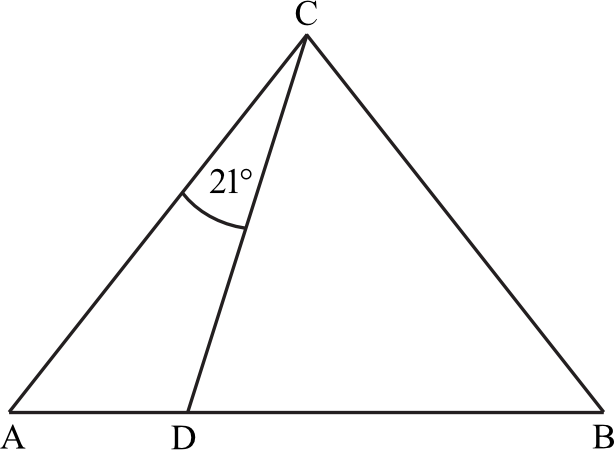
Wynika stąd, że kąt \(BCD\) ma miarę:

A \(57°\)
B \(53°\)
C \(51°\)
D \(55°\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Skoro \(|BD|=|CD|\), to znaczy że trójkąt \(DBC\) jest trójkątem równoramiennym o podstawie \(BC\). Kąty przy podstawie mają jednakową miarę, zatem oznaczmy sobie \(\sphericalangle DBC\) oraz \(\sphericalangle DCB\) jako \(α\). Wiemy też, że \(|AC|=|BC|\), a więc trójkąt \(ABC\) jest również równoramienny i tym samym także ma równe kąty przy podstawie. Jeden z kątów przy podstawie oznaczyliśmy już sobie przed chwilą jako \(α\), więc kąt \(\sphericalangle CAB\) także ma miarę równą \(α\). Krok 2. Obliczenie miary kąta \(BCD\). Aby wyznaczyć miarę kąta \(α\) wystarczy dodać do siebie wszystkie kąty trójkąta \(ABC\), wiedząc że ich suma musi być równa \(180°\). To pozwala nam ułożyć i rozwiązać następujące równanie: $$α+α+21°+α=180° \           ,\ 3α+21°=180° \           ,\ 3α=159° \           ,\ α=53°$$

Teoria:      
W trakcie opracowania