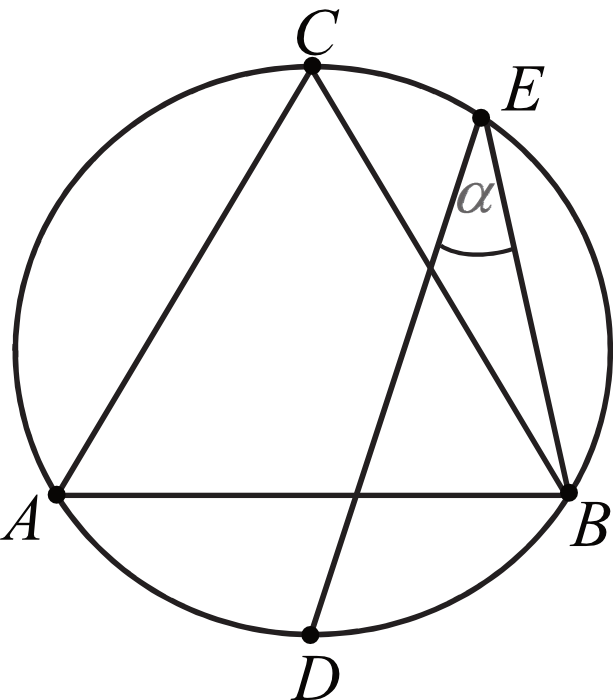
Punkty \(D\) i \(E\) leżą na okręgu opisanym na trójkącie równobocznym \(ABC\) (zobacz rysunek). Odcinek \(CD\) jest średnicą tego okręgu. Kąt wpisany \(DEB\) ma miarę \(α\).

A \(α=30°\)
B \(α\lt30°\)
C \(α\gt45°\)
D \(α=45°\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(DCB\). Odcinek \(CD\) jest średnicą okręgu, a przy okazji będzie też pokrywał się z wysokością trójkąta \(ABC\). W trójkącie równobocznym wysokość trójkąta jest jednocześnie dwusieczną kąta, a to oznacza, że kąt \(DCB\) ma miarę: $$|\sphericalangle DCB|=60°:2 \           ,\ |\sphericalangle DCB|=30°$$ Krok 2. Obliczenie miary kąta \(α\). Kąt \(DCB\) (którego miarę policzyliśmy przed chwilą) oraz \(DEB\) (czyli nasz kąt \(α\)) to kąty oparte na tym samym łuku. Skoro tak, to zgodnie z własnościami kątów wpisanych będą one miały jednakowe miary. To oznacza, że: $$α=30°$$

Teoria:      
W trakcie opracowania