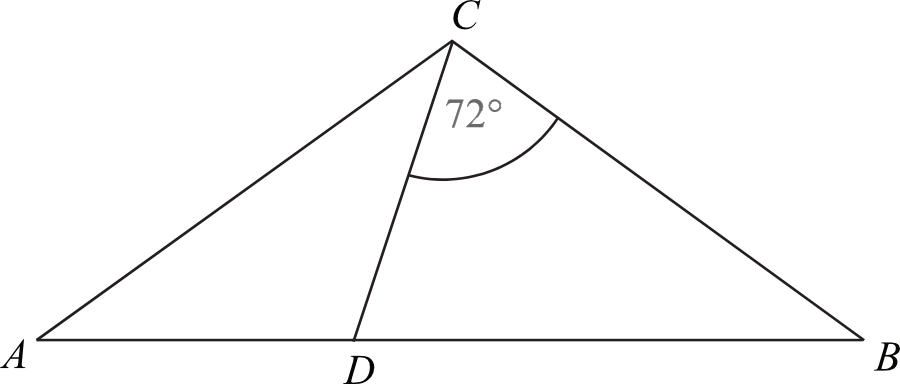
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\). Na podstawie \(AB\) tego trójkąta leży punkt \(D\), taki że \(|AD|=|CD|\), \(|BC|=|BD|\) oraz \(\sphericalangle BCD=72°\) (zobacz rysunek). Wynika stąd, że kąt \(ACD\) ma miarę:

A \(38°\)
B \(36°\)
C \(42°\)
D \(40°\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(CDB\). Spójrzmy na trójkąt \(DBC\). Z treści zadania możemy wywnioskować, że jest to trójkąt równoramienny, ponieważ \(|BC|=|BD|\). Skoro tak, to kąty przy podstawie \(DC\) mają jednakową miarę, a to oznacza, że: $$|\sphericalangle CDB|=72°$$ Krok 2. Obliczenie miary kąta \(ADC\). Kąt \(ADC\) oraz obliczony przed chwilą \(CDB\) to kąty przyległe, czyli takie których suma miar jest równa \(180°\). Możemy więc zapisać, że: $$|\sphericalangle ADC|=180°-72°=108°$$ Krok 3. Obliczenie miary kąta \(ACD\). Teraz spójrzmy na trójkąt \(ADC\). To także jest trójkąt równoramienny, bowiem \(|AD|=|CD|\). Skoro tak, to kąty przy podstawie \(AC\) muszą mieć jednakową miarę. Wiemy już, że kąt \(ADC\) ma miarę \(108°\), czyli na dwa kąty przy podstawie \(AC\) zostaje nam: \(180°-108°=72°\). Skoro kąty przy podstawie \(AC\) muszą być jednakowej miary to: $$|\sphericalangle ACD|=72°:2=36°$$

Teoria:      
W trakcie opracowania