Dany jest prostopadłościan o wymiarach \(30cm\times40cm\times120cm\) (zobacz rysunek), a ponadto dane są cztery odcinki \(a,b,c,d\), o długościach - odpowiednio - \(119cm\), \(121cm\), \(129cm\) i \(131cm\).





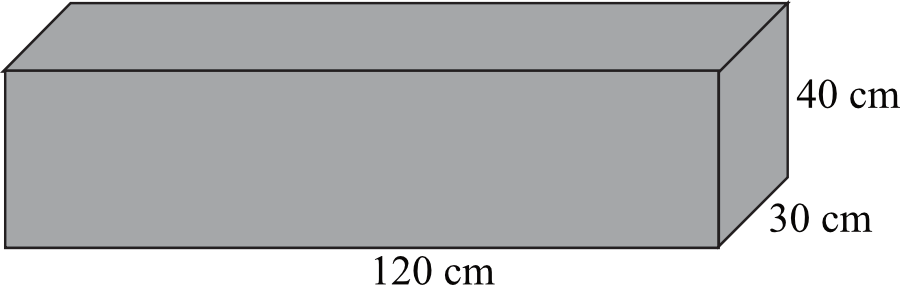
Przekątna tego prostopadłościanu jest dłuższa:

A tylko od odcinka \(a\)
B tylko od odcinków \(a\) i \(b\)
C tylko od odcinków \(a\), \(b\) i \(c\)
D od wszystkich czterech danych odcinków

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Spróbujmy na początek narysować tę sytuację, zaznaczając od razu przekątną całego prostopadłościanu. Utworzył nam się trójkąt prostokątny w którym przekątna bryły jest przeciwprostokątną tego trójkąta. To właśnie z tego trójkąta wyznaczymy długość tej przekątnej. Krok 2. Obliczenie długości przekątnej podstawy. Zanim obliczymy przekątną całego prostopadłościanu to widzimy z rysunku, że musimy obliczyć przekątną podstawy. Korzystając z Twierdzenia Pitagorasa możemy zapisać, że: $$120^2+30^2=c^2 \           ,\ 14400+900=c^2 \           ,\ c^2=15300 \           ,\ c=\sqrt{15300} \quad\lor\quad c=-\sqrt{15300}$$ Ujemną wartość odrzucamy, bo długość boku musi być dodatnia. Zostaje nam więc \(c=\sqrt{15300}\) i na razie w takiej postaci to zostawimy. Krok 3. Obliczenie długości przekątnej prostopadłościanu. Teraz korzystając z naszego zaznaczonego trójkąta prostokątnego możemy obliczyć długość przekątnej całej bryły, ponownie korzystając z Twierdzenia Pitagorasa: $$(\sqrt{15300})^2+40^2=d^2 \           ,\ 15300+1600=d^2 \           ,\ d^2=16900 \           ,\ d=\sqrt{16900} \quad\lor\quad d=-\sqrt{16900} \           ,\ d=130 \quad\lor\quad d=-130$$ Ponownie odrzucamy ujemną długość, zatem zostaje nam \(d=130\). Krok 4. Wybór prawidłowej odpowiedzi. Musimy odpowiedzieć na pytanie od ilu z podanych odcinków nasza przekątna prostopadłościanu jest dłuższa i widzimy wyraźnie, że jest dłuższa od trzech odcinków: \(a\), \(b\) oraz \(c\).

Teoria:      
W trakcie opracowania