W układzie współrzędnych zaznaczono trójkąt \(ABC\) oraz punkt \(P\) należący do boku \(BC\). Wszystkie współrzędne punktów \(A\), \(B\), \(C\) i \(P\) są liczbami całkowitymi.





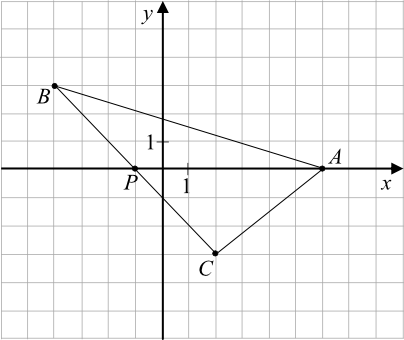
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F - jeśli jest fałszywe. Pole trójkąta \(PAB\) jest równe polu trójkąta \(PAC\).
Pole trójkąta \(ABC\) jest równe \(21\).

Pole trójkąta \(PAB\) jest równe polu trójkąta \(PAC\).

Odpowiedź:      

1) PRAWDA

2) PRAWDA

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni trójkątów \(PAB\) oraz \(PAC\). Zacznijmy od obliczenia pola powierzchni trójkąta \(PAB\). Widzimy wyraźnie (licząc po kratkach), że podstawa tego trójkąta ma długość \(a=7\), natomiast wysokość ma długość \(h=3\) (wysokość to w tym przypadku odległość od wierzchołka \(B\) do osi iksów). To oznacza, że pole tego trójkąta jest równe: $$P_{PAB}=\frac{1}{2}ah \           ,\ P_{PAB}=\frac{1}{2}\cdot7\cdot3 \           ,\ P_{PAB}=10,5$$ Teraz obliczmy pole trójkąta \(PAC\). Tutaj także podstawa ma długość \(a=7\), natomiast wysokość ma długość \(h=3\) (jest to odległość od wierzchołka \(C\) do osi iksów). Pole tego trójkąta będzie więc równe: $$P_{PAC}=\frac{1}{2}ah \           ,\ P_{PAC}=\frac{1}{2}\cdot7\cdot3 \           ,\ P_{PAC}=10,5$$ Krok 2. Ocena prawdziwości pierwszego zdania. Z obliczeń wykonanych w pierwszym kroku wynika, że faktycznie pola powierzchni tych dwóch trójkątów są sobie równe, zatem to zdanie jest prawdą. Krok 3. Ocena prawdziwości drugiego zdania. Pole trójkąta \(ABC\) jest sumą pól trójkątów \(PAB\) oraz \(PAC\), zatem: $$P_{ABC}=P_{PAB}+P_{PAC} \           ,\ P_{ABC}=10,5+10,5 \           ,\ P_{ABC}=21$$ To oznacza, że zdanie jest prawdą.

Teoria:      
W trakcie opracowania