Zbiory arkuszy egzaminacyjnych z matematyki dla ósmoklasistów. Znajdziesz tu różnorodne zadania egzaminacyjne, przykładowe arkusze, rozwiązania zadań, testy z matematyki oraz wiele innych przydatnych materiałów
Egzamin gimnazjalny 2011 - matematyka Zadanie 8 z 12
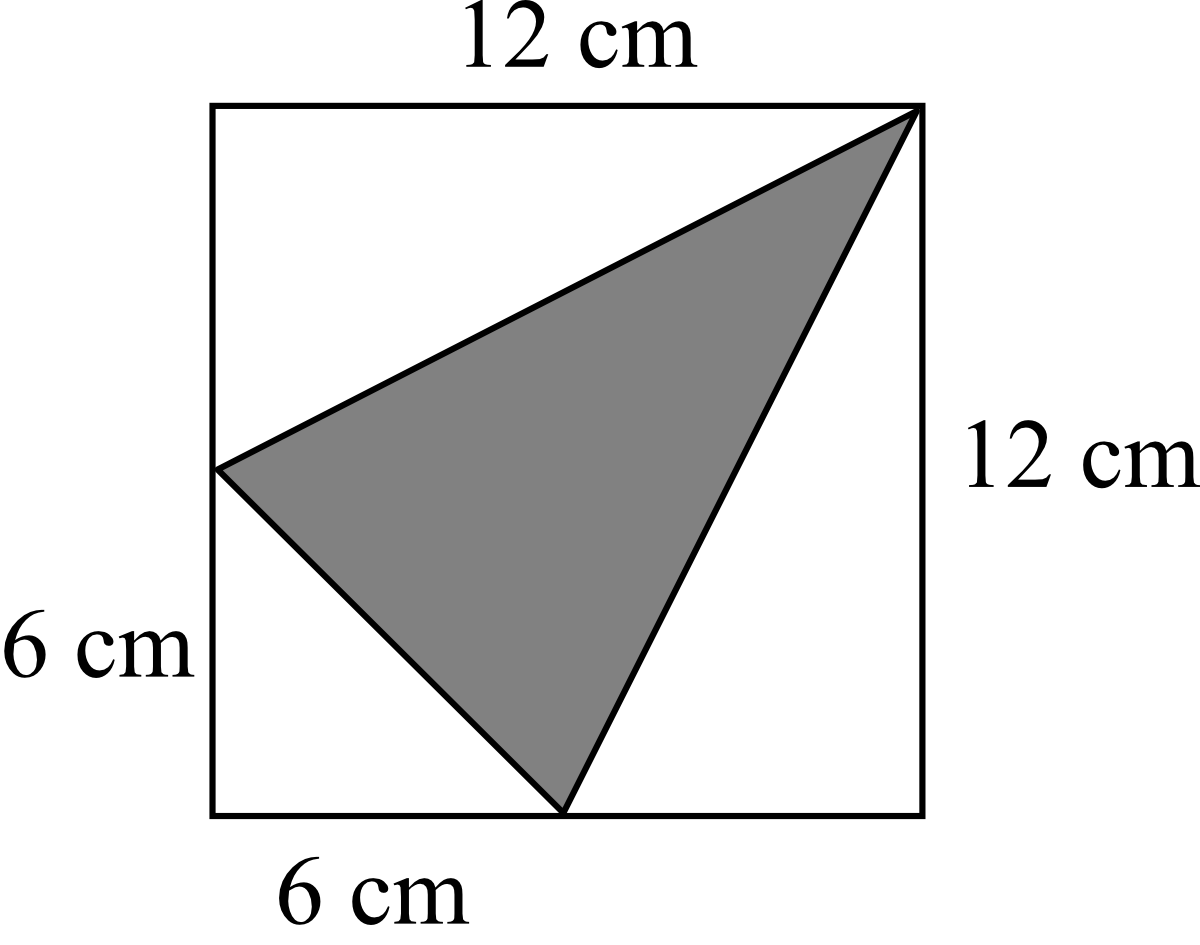
Zadanie nr 8. (1pkt)
Pole zamalowanego trójkąta jest równe:
A \(108cm^2\)
B \(72cm^2\)
C \(54cm^2\)
D \(36cm^2\)
Rozwiązanie:
Krok 1. Obliczenie pól trzech małych trójkątów.
Aby obliczyć pole szarego trójkąta najprościej będzie obliczyć pola trzech małych białych trójkątów, których sumę pól powierzchni odejmiemy od pola kwadratu.
\(P=\frac{1}{2}ah \ ,\
P_{1}=\frac{1}{2}\cdot6\cdot6=\frac{1}{2}\cdot36=18[cm^2] \ ,\
P_{2}=\frac{1}{2}\cdot6\cdot12=\frac{1}{2}\cdot72=36[cm^2] \ ,\
P_{3}=\frac{1}{2}\cdot6\cdot12=\frac{1}{2}\cdot72=36[cm^2]\)
Suma tych trzech pól powierzchni jest równa:
$$P=18+36+36=90cm^2$$
Krok 2. Obliczenie pola kwadratu.
Cały kwadrat ma pole powierzchni równe:
$$P=12\cdot12=144[cm^2]$$
Krok 3. Obliczenie pola powierzchni zamalowanego trójkąta.
Nasz zamalowany trójkąt będzie różnicą między polem powierzchni kwadratu i polem trzech trójkątów, zatem:
$$P=144cm^2-90cm^2=54cm^2$$
Teoria:
W trakcie opracowania
CKE

