Akwarium, w którym Marek hoduje rybki, ma wymiary \(5dm, 8dm, 6dm\). Marek wlewa do niego wodę przepływającą przez kran z szybkością \(8dm^3\) na minutę.





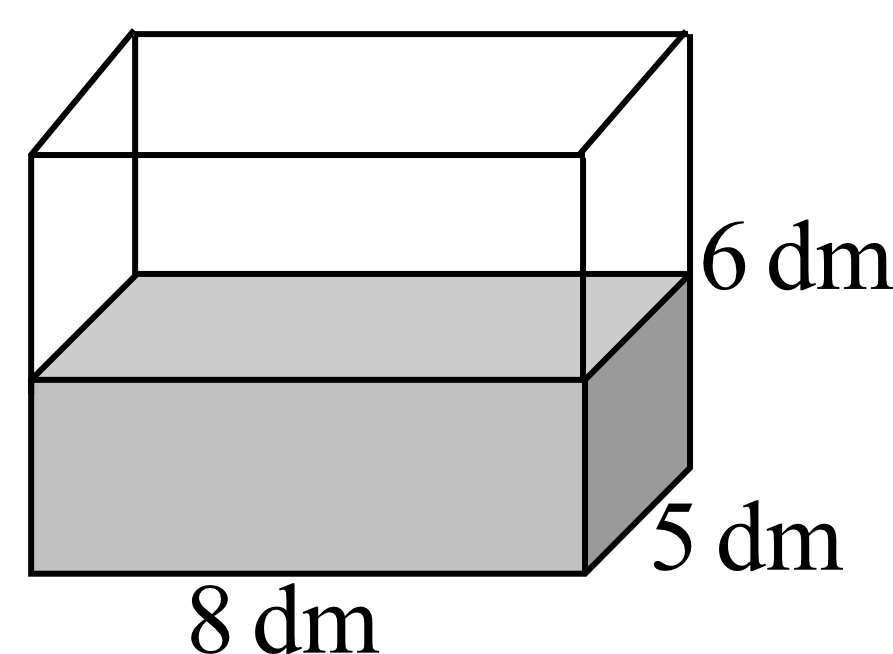
Do jakiej wysokości woda w akwarium będzie sięgać po \(10\) minutach?

Odpowiedź:      

Akwarium będzie sięgać do wysokości \(2dm\).

Rozwiązanie:      
Krok 1. Obliczenie pola podstawy prostopadłościanu. Akwarium jest tak naprawdę prostopadłościanem w którego podstawie znajduje się prostokąt o wymiarach \(8dm\times5dm\). Pole podstawy tego prostopadłościanu jest więc równe: $$P_{p}=8dm\cdot5dm=40dm^2$$ Krok 2. Obliczenie objętości wody. Woda przepływa z prędkością \(8dm^3\) na minutę. Po \(10\) minutach będziemy więc mieć tej wody: $$V=8dm^3\cdot10=80dm^3$$ Krok 3. Obliczenie wysokości sięgania wody. \(80dm^3\) wody wlewa się do prostopadłościanu o podstawie \(40dm^2\). Musimy więc wyliczyć jak wysoko sięgnie ten słup wody, a skorzystamy tutaj ze wzoru na objętość: $$V=P_{p}\cdot H \           ,\ 80dm^3=40dm^2\cdot H \           ,\ H=2dm$$

Teoria:      
W trakcie opracowania