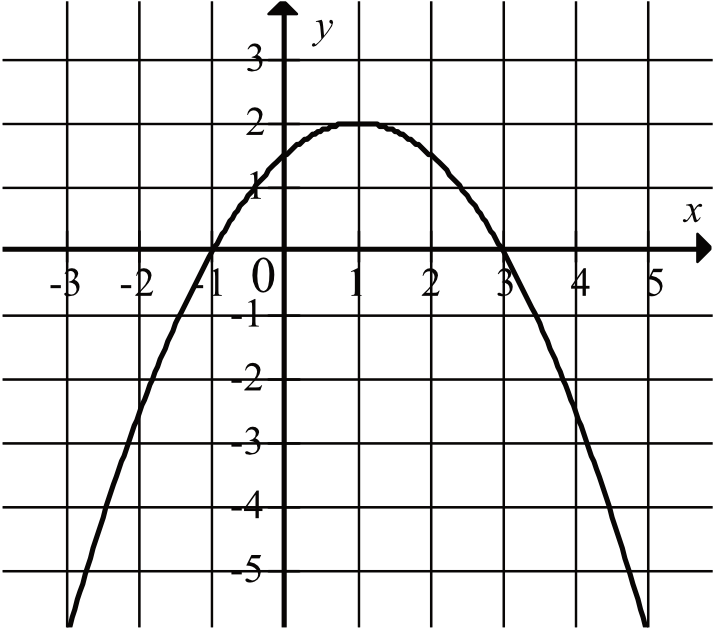
Na rysunku przedstawiono fragment wykresu funkcji kwadratowej \(f\).







Funkcja \(f\) jest określona wzorem:

A \(f(x)=\frac{1}{2}(x+3)(x-1)\)
B \(f(x)=\frac{1}{2}(x-3)(x+1)\)
C \(f(x)=-\frac{1}{2}(x+3)(x-1)\)
D \(f(x)=-\frac{1}{2}(x-3)(x+1)\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Ustalenie wartości współczynnika kierunkowego \(a\). Funkcja ma ramiona paraboli skierowane do dołu, a to oznacza, że współczynnik \(a\) musi być ujemny. To oznacza, że wyboru wzoru musimy dokonać spośród odpowiedzi \(C\) oraz \(D\). Krok 2. Odczytanie miejsc zerowych funkcji. Musimy przedstawić wzór funkcji w postaci iloczynowej typu \(f(x)=a(x-x_{1})(x-x_{2})\), gdzie \(x_{1}\) oraz \(x_{2}\) to miejsca zerowe tej funkcji. Z wykresu odczytujemy, że nasza funkcja ma miejsca zerowe \(x_{1}=3\) oraz \(x_{1}=-1\), a więc jej wzór określimy jako \(f(x)=a(x-3)(x+1)\). Z rozważań zawartych w pierwszym i drugim kroku wynika, że prawidłowym wzorem funkcji jest tylko i wyłącznie ten zawarty w czwartej odpowiedzi - ma on bowiem współczynnik kierunkowy \(a\) mniejszy od zera oraz odpowiada on miejscom zerowym które odczytaliśmy z wykresu funkcji.

Teoria:      
W trakcie opracowania