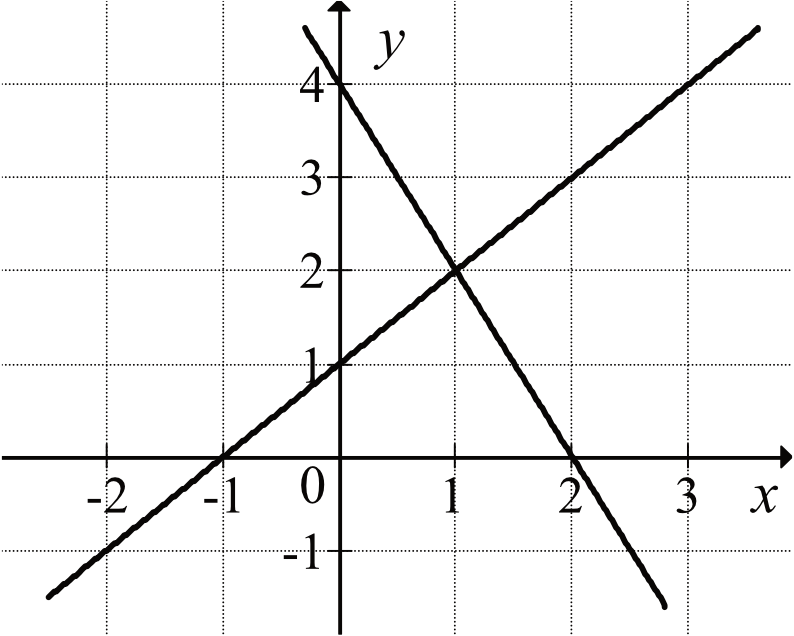Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.







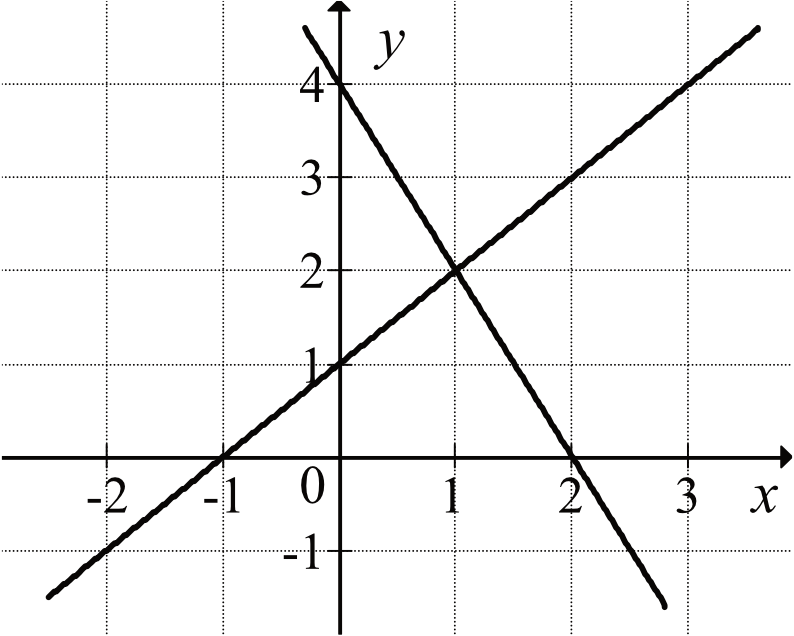
Wskaż ten układ.

A \(\begin{cases}
y=x+1 \           ,\
y=-2x+4
\end{cases}\)
B \(\begin{cases}
y=x-1 \           ,\
y=2x+4
\end{cases}\)
C \(\begin{cases}
y=x-1 \           ,\
y=-2x+4
\end{cases}\)
D \(\begin{cases}
y=x+1 \           ,\
y=2x+4
\end{cases}\)

Odpowiedź:      

A

Rozwiązanie:      
Wszystkie proste przedstawione są w postaci \(y=ax+b\), a naszym zadaniem jest tak naprawdę odczytanie z rysunku potrzebnych informacji i ustalenie poszczególnych współczynników \(a\) oraz \(b\). Krok 1. Ustalenie wzoru pierwszej prostej (rosnącej). Jeśli przyjrzymy się odpowiedziom to pierwsza prosta jest przedstawiona w dwóch wariantach: \(y=x+1\) lub \(y=x-1\). Musimy więc tak naprawdę ustalić współczynnik \(b\) tej prostej i dowiedzieć się, czy jest on równy \(1\), czy \(-1\). Współczynnik \(b\) mówi nam o tym w którym miejscu z osią \(Oy\) przetnie się wykres prostej. W naszym przypadku przeciął się on w punkcie \((0;1)\), a więc \(b=1\). To oznacza, że pierwsza prosta ma na pewno postać \(y=x+1\). Krok 2. Ustalenie wzoru drugiej prostej (malejącej). Druga prosta jest opisana w odpowiedziach na dwa sposoby: \(y=2x+4\) lub \(y=-2x+4\). To znaczy, że musimy tym razem zweryfikować wartość współczynnika \(a\) i stwierdzić, czy jest on równy \(2\), czy może \(-2\). Skoro prosta jest malejąca, to bez żadnych zbędnych obliczeń jesteśmy w stanie stwierdzić, że prosta jest malejąca, czyli \(a=-2\). Przy okazji widzimy też, że współczynnik \(b=4\), bo prosta ta przecina oś \(Oy\) w punkcie \((0;4)\), więc z całą pewnością wzorem tej prostej jest \(y=-2x+4\). To oznacza, że poszukiwanym przez nas układem jest ten z pierwszej odpowiedzi.

Teoria:      
W trakcie opracowania