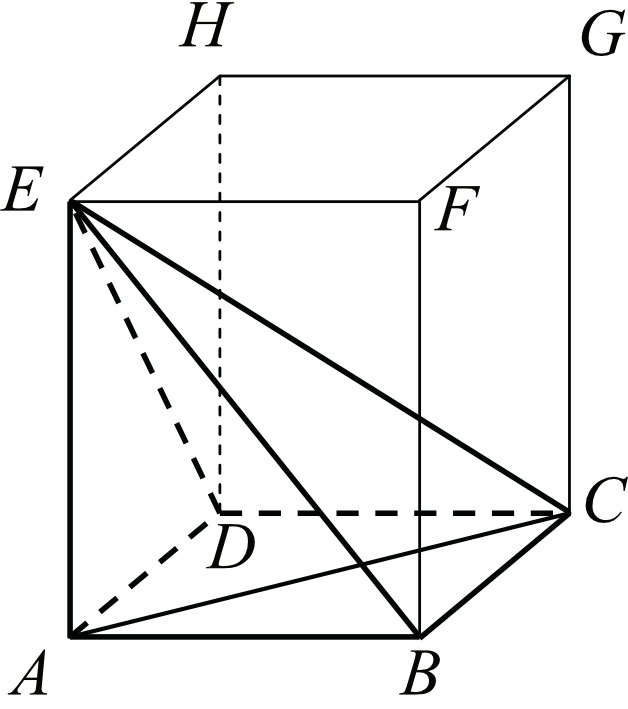
W graniastosłupie prawidłowym czworokątnym \(ABCDEFGH\) przekątna \(AC\) podstawy ma długość \(4\). Kąt \(ACE\) jest równy \(60°\). Oblicz objętość ostrosłupa \(ABCDE\) przedstawionego na poniższym rysunku.

Odpowiedź:      

\(V=\frac{32\sqrt{3}}{3}\)

Rozwiązanie:      
Krok 1. Obliczenie wysokości graniastosłupa. Skorzystamy tutaj z trójkąta prostokątnego \(ACE\). Znamy długość \(|AC|=4\) i znamy też miarę jednego z kątów \(|\sphericalangle ACE|=60°\). Te dwie dane posłużą nam do wyznaczenia wysokości graniastosłupa (czyli \(AE\)), a skorzystamy tutaj z funkcji tangensa: $$tg60°=\frac{|AE|}{|AC|} \           ,\ \sqrt{3}=\frac{|AE|}{4} \           ,\ |AE|=4\sqrt{3}$$ Krok 2. Obliczenie długości krawędzi podstawy. Skoro jest to graniastosłup prawidłowy czworokątny, to znaczy że w swojej podstawie ma on kwadrat. Znamy przekątną tego kwadratu i jest ona równa \(d=|AC|=4\). Z własności kwadratu wiemy też, że \(d=a\sqrt{2}\), a to pozwoli nam szybko wyliczyć długość krawędzi podstawy: $$4=a\sqrt{2} \           ,\ a=\frac{4}{\sqrt{2}}=\frac{4\cdot\sqrt{2}}{\sqrt{2}\cdot\sqrt{2}}=\frac{4\sqrt{2}}{2}=2\sqrt{2}$$ Ta długość przyda nam się teraz do obliczenia pola podstawy. Krok 3. Obliczenie pola podstawy. Skoro w podstawie mamy kwadrat o boku \(a=2\sqrt{2}\), to pole podstawy będzie równe: $$P_{p}=(2\sqrt{2})^2=4\cdot2=8$$ Krok 4. Obliczenie objętości wyznaczonego ostrosłupa. Musimy teraz obliczyć objętość ostrosłupa. Znamy jego wysokość \(h=4\sqrt{3}\), obliczyliśmy także że \(P_{p}=8\), więc wystarczy już tylko podstawić te dane do standardowego wzoru na objętosć ostrosłupów: $$V=\frac{1}{3}\cdot P_{p}\cdot H \           ,\ V=\frac{1}{3}\cdot8\cdot4\sqrt{3} \           ,\ V=\frac{32\sqrt{3}}{3}$$

Teoria:      
W trakcie opracowania