Na rysunku przedstawiono fragment wykresu funkcji \(f\), który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem \(y=\frac{1}{x}\) dla każdej liczby rzeczywistej \(x\neq0\).







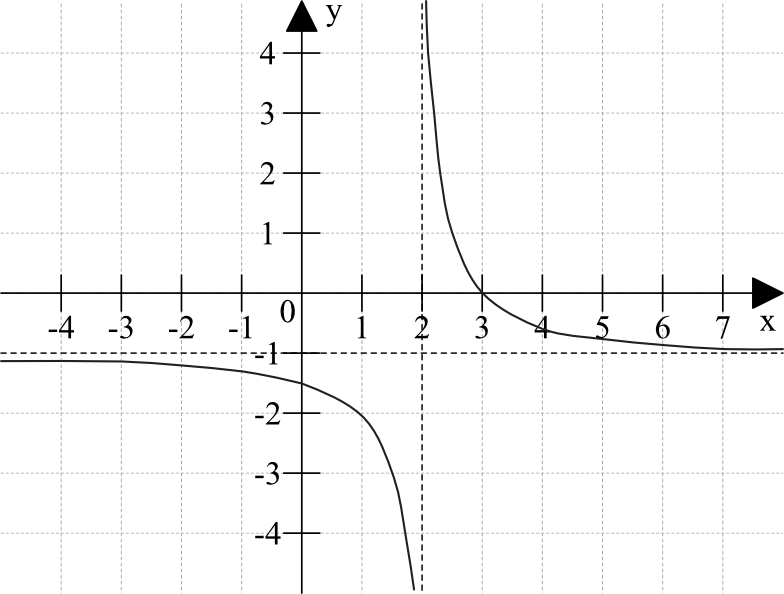
a) Odczytaj z wykresu i zapisz zbiór tych wszystkich argumentów, dla których wartości funkcji \(f\) są większe od \(0\).

b) Podaj miejsce zerowe funkcji \(g\) określonej wzorem \(g(x)=f(x-3)\).

Odpowiedź:      

a) \(x\in(2;3)\)
b) \(x=6\)

Rozwiązanie:      
Krok 1. Podanie pożądanego zbioru argumentów. Z wykresu możemy odczytać, że funkcja przyjmuje wartości większe od zera tylko dla \(x\in(2;3)\). Krok 2. Podanie miejsca zerowego dla funkcji \(g(x)=f(x-3)\). Nasza funkcja \(f(x)\) ma tylko jedno miejsce zerowe i jest to \(x=3\). Przesunięcie tej funkcji o trzy jednostki w prawo (a tak będzie wyglądać funkcja \(g(x)\)) sprawi, że miejsce zerowe nadal będzie jedno i tym razem będzie to \(x=6\).

Teoria:      
W trakcie opracowania