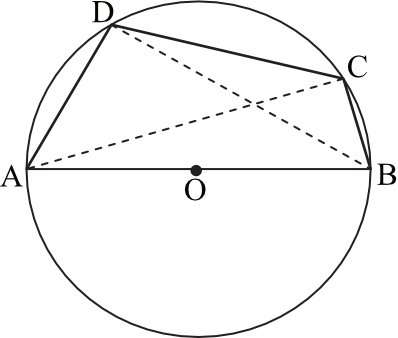
Bok AB czworokąta \(ABCD\) wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że \(|AD|^2+|BD|^2=|BC|^2+|AC|^2\).

Odpowiedź:      

Udowodniono wykorzystując własności trójkątów opartych na średnicy oraz wykorzystując Twierdzenie Pitagorasa.

Rozwiązanie:      
Kluczem do rozwiązania tego zadania jest dostrzeżenie, że trójkąty \(ABC\) i \(ABD\) są prostokątne. Skąd to wiemy? Obydwa trójkąty wyznaczone przez przekątne czworokąta są oparte na średnicy okręgu, a z własności figur w okręgach wiemy, że to jest równoznaczne z tym że dany trójkąt jest prostokątny. Tak więc: $$\sphericalangle ADB|=|\sphericalangle ACB|=90°$$ Skoro są to trójkąty prostokątne to do udowodnienia tezy zawartej w zadaniu możemy skorzystać z Twierdzenia Pitagorasa, tworząc prosty układ równań: \begin{cases} \text{Trójkąt }ABD: |AD|^2+|BD|^2=|AB|^2 \           ,\ \text{Trójkąt }ABC: |BC|^2+|AC|^2=|AB|^2 \end{cases} Po prawej stronie tych dwóch równań mamy wartość \(|AB|^2\), więc korzystając z metody podstawiania otrzymamy: $$|AD|^2+|BD|^2=|BC|^2+|AC|^2$$ Co należało udowodnić.

Teoria:      
W trakcie opracowania