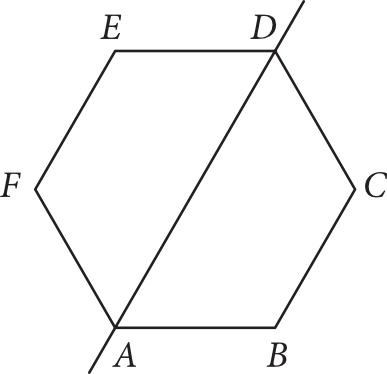
Punkty \(A=(-2\sqrt{3},0)\), \(B=(0,0)\), \(C=(\sqrt{3},3)\) są kolejnymi wierzchołkami sześciokąta foremnego \(ABCDEF\). Wyznacz równanie prostej zawierającej przekątną \(AD\) tego sześciokąta.

Odpowiedź:      

\(y=\sqrt{3}x+6\)

Rozwiązanie:      
Krok 1. Wyznaczenie współczynnika kierunkowego \(a\) prostej \(BC\). Kluczem do rozwiązania tego zadania jest dostrzeżenie, że proste \(BC\) oraz \(AD\) są względem siebie równoległe. Jeżeli więc wyznaczymy współczynnik kierunkowy \(a\) prostej \(BC\) (a nie jest to trudne, bo znamy współrzędne punktów \(B\) oraz \(C\)), to będziemy bardzo blisko odnalezienia równania prostej przechodzącej przez przekątną \(AD\). Oczywiście możemy wyznaczyć całe równanie prostej \(BC\) (np. z metody układu równań), ale nam wystarczy poznanie współczynnika \(a\) tej prostej, a dokonamy tego za pomocą prostego wzoru: $$a=\frac{y_{C}-y_{B}}{x_{C}-x_{B}} \           ,\ a=\frac{3-0}{\sqrt{3}-0} \           ,\ a=\frac{3}{\sqrt{3}} \           ,\ a=\frac{3\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}} \           ,\ a=\frac{3\sqrt{3}}{3} \           ,\ a=\sqrt{3}$$ Krok 2. Wyznaczenie równania prostej \(AD\). Wiemy, że prosta \(AD\) jest równoległa do prostej \(BC\), zatem współczynnik kierunkowy \(a\) tej prostej będzie równy \(\sqrt{3}\). Możemy więc powiedzieć, że nasza prosta będzie się wyrażać równaniem \(y=\sqrt{3}x+b\). Musimy jeszcze poznać wartość współczynnika \(b\), a dokonamy tego podstawiając współrzędne punktu przez które ta prosta przechodzi, czyli punktu \(A=(-2\sqrt{3},0)\): $$y=\sqrt{3}x+b \           ,\ 0=\sqrt{3}\cdot(-2\sqrt{3})+b \           ,\ 0=-2\cdot3+b \           ,\ b=6$$ Skoro współczynnik \(b=6\), to nasza prosta \(AD\) wyraża się równaniem \(y=\sqrt{3}x+6\).

Teoria:      
W trakcie opracowania