W tabeli podano oceny z matematyki czterech uczniów pewnej klasy.





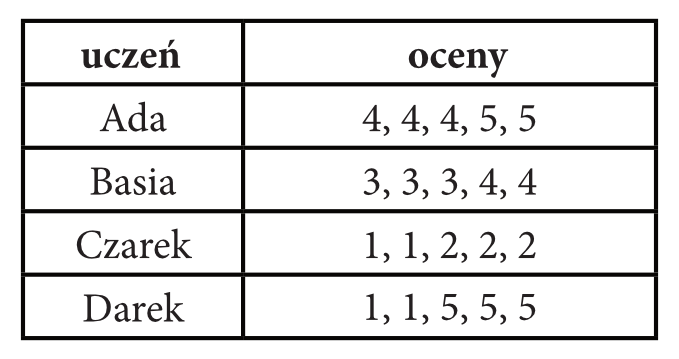
Oceny którego ucznia wykazują największe odchylenie standardowe?

A Ady
B Basi
C Czarka
D Darka

Odpowiedź:      

D

Rozwiązanie:      
Odchylenie standardowe możemy obliczyć korzystając np. ze wzoru: \(\begin{split}σ=\sqrt{\frac{{x_{1}}^2+{x_{2}}^2+...+{x_{n}}^2}{n}-(\bar{a})^2}\end{split}\) Musielibyśmy więc obliczyć średnią arytmetyczną dla każdego ucznia (to jest to właśnie \(\bar{a}\) znajdujące się we wzorze), a następnie musielibyśmy podstawiać do tego wzoru poszczególne oceny. Jest to dość sporo liczenia, ale tak przykładowo dla Ady obliczenia wyglądałyby następująco: $$\bar{a}=\frac{4+4+4+5+5}{5} \           ,\ \bar{a}=\frac{22}{5} \           ,\ \bar{a}=4,4$$ Odchylenie standardowe wyniosłoby więc: $$\begin{split}σ=\sqrt{\frac{4^2+4^2+4^2+5^2+5^2}{5}-(4,4^2)}\end{split} \           ,\ \begin{split}σ=\sqrt{\frac{16+16+16+25+25}{5}-19,36}\end{split} \           ,\ \begin{split}σ=\sqrt{\frac{98}{5}-19,36}\end{split} \           ,\ \begin{split}σ=\sqrt{\frac{98}{5}-19,36}\end{split} \           ,\ σ=\sqrt{19,6-19,36} \           ,\ σ=\sqrt{0,24} \           ,\ σ\approx0,49$$ Jednak do tego zadania powinniśmy podejść nieco inaczej. To zadanie tak prawdę mówiąc bardziej sprawdza to, czy rozumiemy czym jest odchylenie standardowe. Powinniśmy zauważyć, że odchylenie standardowe jest tym większe im bardziej poszczególne liczby odstają od średniej. Oceny Ady, Basi i Czarka są niemalże jednolite. Oceny Darka są już bardziej "rozstrzelone", bo Darek ma same skrajne oceny. To sprawia, że każda z ocen będzie mocno odstawać od średniej arytmetycznej i tym samym odchylenie standardowe będzie tutaj bardzo wysokie. To właśnie dlatego bez żadnego liczenia możemy powiedzieć, że odchylenie standardowe ocen Darka będzie zdecydowanie największe.

Teoria:      
W trakcie opracowania