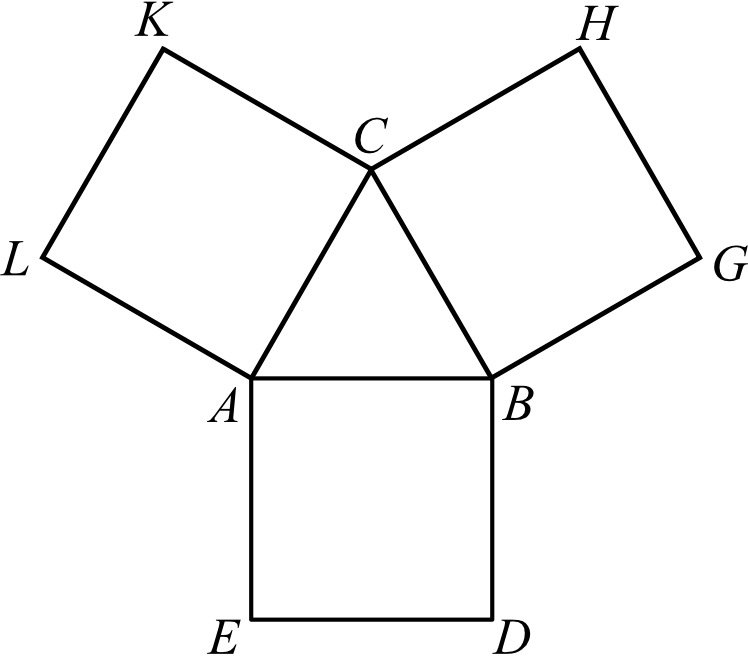
Na bokach trójkąta równobocznego \(ABC\) (na zewnątrz tego trójkąta) zbudowano kwadraty \(ABDE\), \(CBGH\), \(ACKL\). Udowodnij, że trójkąt \(KGE\) jest równoboczny.

Odpowiedź:      

Udowodniono korzystając z cech przystawania trójkątów.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Spróbujmy połączyć ze sobą punkty \(LE\), \(DG\) oraz \(KH\). Powstaną nam wtedy trzy trójkąty \(ΔLEA\), \(ΔDGB\) oraz \(ΔKCH\) i będą to trójkąty równoramienne (bo ramionami są boki identycznych kwadratów). Możemy nawet obliczyć miarę tego kąta rozwartego każdego z tych trójkątów i będzie to \(120°\). Skąd to wiemy? Spójrzmy na poniższy rysunek i na kąt \(\sphericalangle LAE\). W skład kąta pełnego wchodzą dwa kąty z kwadratów, kąt z trójkąta równobocznego oraz nasz kąt rozwarty \(\sphericalangle LAE\), zatem: $$|\sphericalangle LAE|=360°-90°-90°-60°=120°$$ Analogicznie możemy przeanalizować kąty \(\sphericalangle DBG\) oraz \(\sphericalangle KCH\). To z kolei prowadzi nas do bardzo ważnego wniosku - skoro trójkąty \(ΔLAE\), \(ΔDGB\) oraz \(ΔKCH\) mają te same długości ramion i mają taki sam kąt między ramionami, to na pewno są to trójkąty przystające (cecha bok-kąt-bok). Tutaj warto też nadmienić, że kąty przy niebieskich podstawach będą mieć \(30°\). Skąd to wiemy? Są to trójkąty równoramienne, a kąt między ich ramionami wynosi \(120°\), zatem każdy z kątów przy podstawie musi mieć: \((180°-120°):2=30°\). Ta wiedza przyda nam się w drugim kroku. Krok 2. Udowodnienie, że trójkąty \(ΔEDG\), \(ΔKHG\), \(ΔLKE\) są przystające i zakończenie dowodzenia. Spójrzmy teraz na kolejny rysunek: Z pierwszego kroku wynika, że odcinki \(LE\), \(DG\) oraz \(KH\) są sobie równe. Równe też są na pewno odcinki \(LK\), \(ED\) oraz \(HG\), bo są to boki kwadratów. Widzmy także, że kąty: $$|\sphericalangle KLE|=|\sphericalangle EDG|=|\sphericalangle KHG|=90°+30°=120°$$ To oznacza, że trójkąty \(ΔEDG\), \(ΔKHG\), \(ΔLKE\) są także trójkątami przystającymi, a skoro tak, to mają identyczne długości odcinków \(|KE|=|EG|=|GK|\), co jest dowodem na to, że trójkąt \(ΔKGE\) jest równoboczny.

Teoria:      
W trakcie opracowania