Punkty \(D\) i \(E\) są środkami przyprostokątnych \(AC\) i \(BC\) trójkąta prostokątnego \(ABC\). Punkty \(F\) i \(G\) leżą na przeciwprostokątnej \(AB\) tak, że odcinki \(DF\) i \(EG\) są do niej prostopadłe (zobacz rysunek). Pole trójkąta \(BGE\) jest równe \(1\), a pole trójkąta \(AFD\) jest równe \(4\).







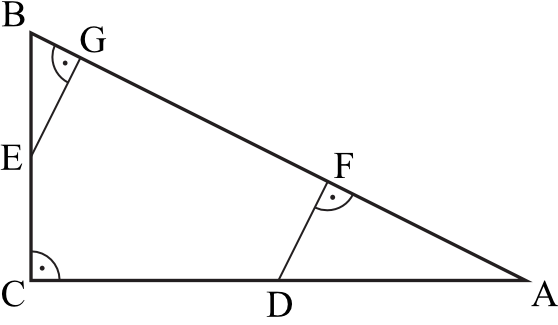
Zatem pole trójkąta \(ABC\) jest równe:

A \(12\)
B \(16\)
C \(18\)
D \(20\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Dorysowalismy sobie wysokość \(CH\) trójkąta \(ABC\). Podzieliła nam ona trójkąt na dwa mniejsze trójkąty - \(ACH\) oraz \(BCH\). Suma pól powierzchni tych trójkątów da nam poszukiwane pole trójkąta \(ABC\). Krok 2. Obliczenie pola powierzchni trójkąta \(ACH\). Skorzystamy tutaj ze skali podobieństwa trójkątów \(ACH\) oraz \(AFD\). Z treści zadania wynika, że \(k=\frac{|AC|}{|AD|}=2\). Z geometrii wiemy, że stosunek dwóch pól figur podobnych jest równy \(k^2\), czyli w naszym przypadku \(k^2=2^2=4\). Skoro pole trójkąta \(AFD\) jest równe \(4\), a pole \(ACH\) musi być czterokrotnie większe, to \(P_{ACH}=4\cdot4=16\). Krok 3. Obliczenie pola powierzchni trójkąta \(BCH\). Analogicznie możemy przeanalizować parę trójkątów \(BCH\) oraz \(BGE\). Skoro \(k=\frac{|BH|}{|BG|}=2\), to ponownie pole trójkąta \(BCH\) będzie czterokrotnie większe od pola trójkąta \(BGE\). Pole trójkąta \(BCH\) jest więc równe \(P_{BCH}=4\cdot1=4\). Krok 4. Obliczenie pola powierzchni trójkąta \(ABC\). $$P_{ABC}=P_{ACH}+P_{BCH} \           ,\ P_{ABC}=16+4 \           ,\ P_{ABC}=20$$

Teoria:      
W trakcie opracowania