Punkty \(A, B, C\) leżą na okręgu o środku \(O\) (jak na rysunku), przy czym krótszy z łuków \(AB\) stanowi \(\frac{2}{5}\) okręgu.





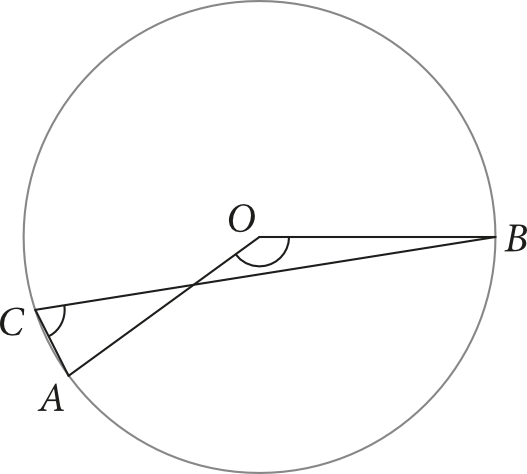
Suma miar kątów \(AOB\) i \(ACB\) jest równa:

A \(144°\)
B \(180°\)
C \(210°\)
D \(216°\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(AOB\). Kąt \(AOB\) jest kątem środkowym, opartym na łuku o długości \(\frac{2}{5}\) obwodu okręgu. To oznacza, że miara tego kąta będzie stanowić \(\frac{2}{5}\) miary kąta pełnego, zatem: $$|\sphericalangle AOB|=\frac{2}{5}\cdot360° \           ,\ |\sphericalangle AOB|=144°$$ Krok 2. Obliczenie miary kąta \(ACB\). Choć może nie widać tego na pierwszy rzut oka (zwłaszcza że odcinek \(AC\) trochę zlewa się z krawędzią okręgu), to kąt \(ACB\) jest kątem wpisanym opartym dokładnie na tym samym łuku \(AB\) co nasz kąt środkowy \(AOB\). Z własności kątów środkowych i wpisanych wiemy, że w takiej sytuacji miara naszego kąta wpisanego musi być dwa razy mniejsza od kąta środkowego, zatem: $$|\sphericalangle ACB|=144°:2 \           ,\ |\sphericalangle ACB|=72°$$ Krok 3. Obliczenie sumu miar kątów \(AOB\) oraz \(ACB\). Pytają się nas o to jaka jest suma tych dwóch analizowanych przed chwilą kątów, zatem odpowiedzią do tego zadania będzie: $$144°+72°=216°$$

Teoria:      
W trakcie opracowania