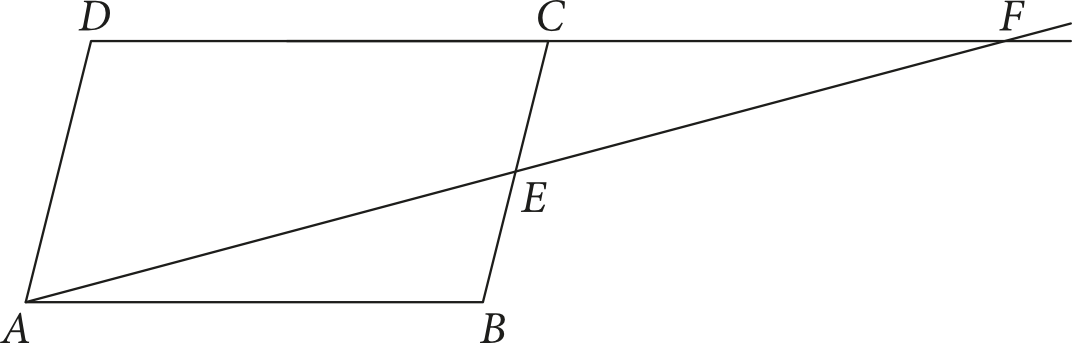
W równoległoboku \(ABCD\) punkt \(E\) jest środkiem boku \(BC\). Przez punkty \(A\) i \(E\) poprowadzono prostą przecinającą prostą \(DC\) w punkcie \(F\) (jak na rysunku). Uzasadnij, że pole równoległoboku \(ABCD\) jest równe polu trójkąta \(AFD\).

Odpowiedź:      

Udowodniono korzystając z cech trójkątów przyległych.

Rozwiązanie:      
Krok 1. Dostrzeżenie przystawania trójkątów. Powinniśmy dostrzec, że trójkąty \(ABE\) oraz \(EFC\) są przystające. Skąd to wiemy? Na pewno kąty \(AEB\) oraz \(CEF\) są jednakowej miary (bo są to kąty wierzchołkowe). Kąty \(EBA\) oraz \(ECF\) także są jednakowej miary, bo są to kąty naprzemianległe. Dodatkowo wiemy, że punkt \(E\) jest środkiem odcinka \(BC\), czyli odcinek \(BE\) ma taką samą długość co \(CE\). Z tej powyższej analizy wynika, że w trójkątach \(ABE\) oraz \(EFC\) mamy dwie pary jednakowych kątów i jedną parę boków o jednakowej długości. Zgodnie więc z cechą kąt-bok-kąt jesteśmy w stanie stwierdzić, że te trójkąty są nie tylko podobne, ale wręcz przystające (czyli są to tak naprawdę jednakowe trójkąty). To z kolei oznacza, że trójkąt \(EFC\) ma jednakowe pole powierzchni co trójkąt \(ABE\), stąd też właśnie duży trójkąt \(AFD\) ma jednakowe pole powierzchni, co równoległobok \(ABCD\).

Teoria:      
W trakcie opracowania