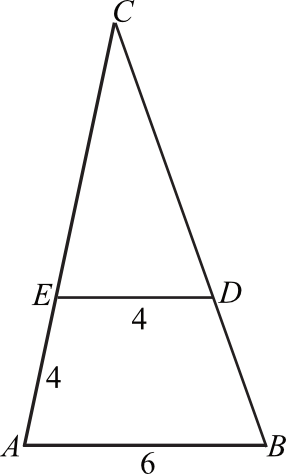W trójkącie \(ABC\) punkt \(D\) leży na boku \(BC\), a punkt \(E\) leży na boku \(AC\). Odcinek \(DE\) jest równoległy do boku \(AB\), a ponadto \(|AE|=|DE|=4\), \(|AB|=6\) (zobacz rysunek).





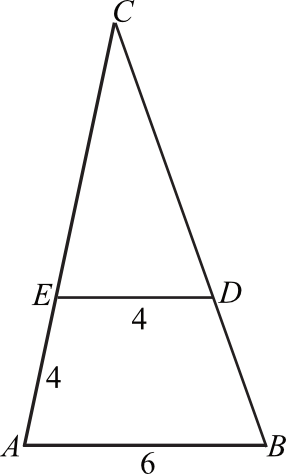
Odcinek \(CE\) ma długość:

A \(\frac{16}{3}\)
B \(\frac{8}{3}\)
C \(8\)
D \(6\)

Odpowiedź:      

C

Rozwiązanie:      
Trójkąty \(ABC\) oraz \(EDC\) są podobne (cecha kąt-kąt-kąt), zatem możemy zapisać prostą propocję: $$\frac{|CA|}{|AB|}=\frac{|CE|}{|ED|} \           ,\ \frac{|CE|+4}{6}=\frac{|CE|}{4}$$ Mnożąc na krzyż otrzymamy: $$4\cdot(|CE|+4)=6|CE| \           ,\ 4|CE|+16=6|CE| \           ,\ 16=2|CE| \           ,\ |CE|=8$$

Teoria:      
W trakcie opracowania