Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura próbna z matematyki (poziom podstawowy) - Kwiecień 2020 Zadanie 14 z 34
Zadanie nr 14. (1pkt)
Na okręgu o środku w punkcie \(O\) leżą punkty \(A\), \(B\) i \(C\) (zobacz rysunek). Kąt \(ABC\) ma miarę \(121°\), a kąt \(BOC\) ma miarę \(40°\).
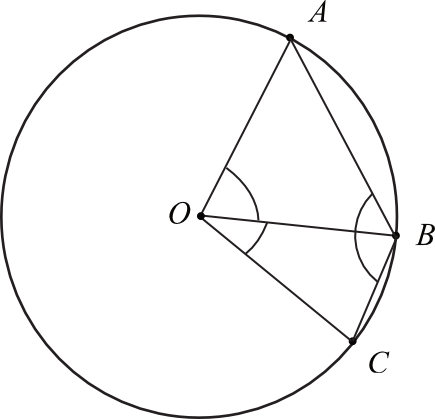
Kąt \(AOB\) ma miarę:
A \(59°\)
B \(50°\)
C \(81°\)
D \(78°\)
Rozwiązanie:
Krok 1. Wyznaczenie miary kąta \(CBO\).
Na wstępie musimy dostrzec, że trójkąty \(BCO\) oraz \(ABO\) są równoramienne, bo ich ramiona mają długość równą promieniowi okręgu. Spójrzmy zatem na trojkąt \(BCO\). Wiemy, że kąt \(BOC\) ma miarę \(40°\), a to oznacza, że kąt \(CBO\) znajdujący się przy podstawie ma miarę:
$$|\sphericalangle CBO|=(180°-40°):2=140°:2=70°$$
Krok 2. Wyznaczenie miary kąta \(ABO\).
Wiemy, że kąt \(ABC\) ma miarę \(121°\) i widzimy na rysunku, że składa się on z kątów \(CBO\) oraz \(ABO\). Miarę kąta \(CBO\) wyliczyliśmy przed chwilą, zatem:
$$|\sphericalangle ABO|=121°-70°=51°$$
Krok 3. Wyznaczenie miary kąta \(AOB\).
Spójrzmy teraz na trójkąt \(ABO\). Wiemy że kąty przy podstawie mają tutaj \(51°\), bo jest to trójkąt równoramienny, zatem kąt \(AOB\) ma miarę:
$$|\sphericalangle AOB|=180°-2\cdot51°=180°-102°=78°$$
Teoria:
W trakcie opracowania
matura próbna - CKE

