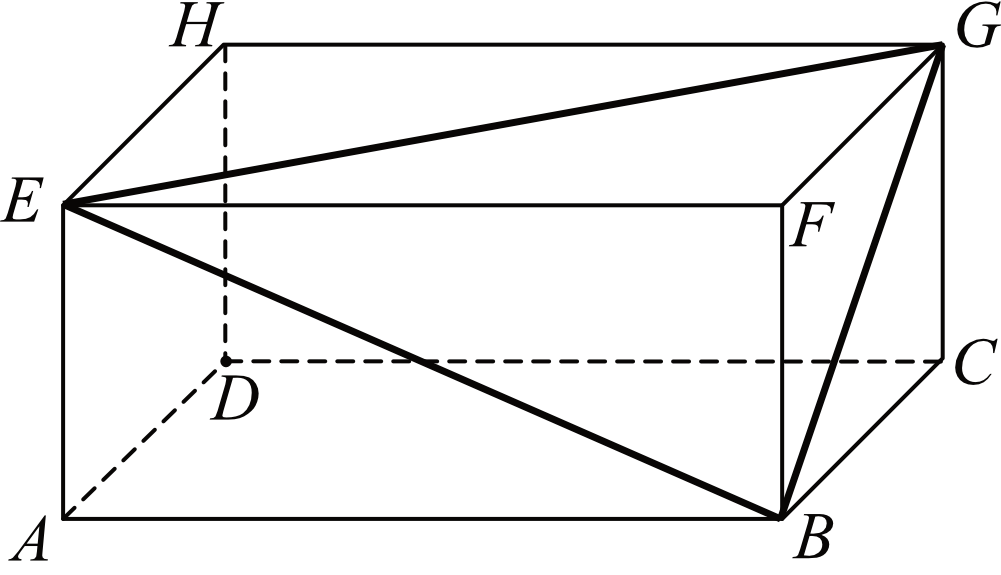
W prostopadłościanie \(ABCDEFGH\) mamy: \(|AB|=5\), \(|AD|=4\), \(|AE|=3\). Który z odcinków \(AB\), \(BG\), \(GE\), \(EB\) jest najdłuższy?

A \(AB\)
B \(BG\)
C \(GE\)
D \(EB\)

Odpowiedź:      

C

Rozwiązanie:      
Wiemy, że \(|AB|=5\). Pozostałe długości boków musimy obliczyć korzystając z Twierdzenia Pitagorasa \(a^2+b^2=c^2\) oraz z długości odcinków podanych w zadaniu. Krok 1. Obliczenie długości odcinka \(BG\). $$|BG|^2=|FB|^2+|FG|^2 \           ,\ |BG|^2=3^2+4^2 \           ,\ |BG|^2=9+16 \           ,\ |BG|^2=25 \           ,\ |BG|=5$$ Krok 2. Obliczenie długości odcinka \(GE\). $$|GE|^2=|FE|^2+|FG|^2 \           ,\ |GE|^2=5^2+4^2 \           ,\ |GE|^2=25+16 \           ,\ |GE|^2=41 \           ,\ |GE|=\sqrt{41}$$ Krok 3. Obliczenie długości odcinka \(EB\). $$|EB|^2=|AB|^2+|AE|^2 \           ,\ |EB|^2=5^2+3^2 \           ,\ |EB|^2=25+9 \           ,\ |EB|^2=34 \           ,\ |EB|=\sqrt{34}$$ Krok 4. Wskazanie najdłuższego odcinka. Sprowadźmy wszystkie odpowiedzi do jakiejś wspólnej postaci, np. pierwiastka: $$|AB|=5=\sqrt{25} \           ,\ |BG|=5=\sqrt{25} \           ,\ |GE|=\sqrt{41} \           ,\ |EB|=\sqrt{34}$$ W związku z tym widzimy, że najdłuższy jest odcinek \(GE\).

Teoria:      
W trakcie opracowania