Drabinę o długości \(4\) metrów oparto o pionowy mur, a jej podstawę umieszczono w odległości \(1,30m\) od tego muru (zobacz rysunek).







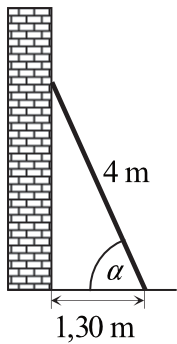
Kąt \(α\), pod jakim ustawiono drabinę, spełnia warunek:

A \(0°\lt α\lt 30°\)
B \(30°\lt α\lt 45°\)
C \(45°\lt α\lt 60°\)
D \(60°\lt α\lt 90°\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Wyznaczenie wartości \(cosα\). Z funkcji trygonometrycznych w trójkącie prostokątnym wynika, że zależność między przyprostokątną leżącą przy danym kącie, a przeciwprostokątną możemy opisać funkcją cosinus: $$cosα=\frac{1,30}{4} \           ,\ cosα=0,325$$ Krok 2. Odczytanie miary kąta z tablic trygonometrycznych. Musimy teraz poprawnie odczytać z tablic trygonometrycznych dla jakiego kąta ostrego funkcja cosinus przyjmuje wartość około \(0,325\). Najbliżej tej wartości jest kąt \(71°\), zatem \(60°\lt α\lt 90°\). Uwaga! Wiele osób błędnie odczytuje z tablic, że poszukiwanym kątem jest ten o mierze \(19°\). To byłby kąt \(19°\) gdybyśmy mieli funkcję sinus, a nie cosinus.

Teoria:      
W trakcie opracowania