Adam mieszka w miejscowości Bocianowo, a jego kolega Bartek – w miejscowości Żabno. Adam umówił się z Bartkiem w Żabnie na godzinę 18:00. Wyjechał z Bocianowa na skuterze o godzinie 17:20. Średnia prędkość jazdy Adama była równa \(25\frac{km}{h}\).



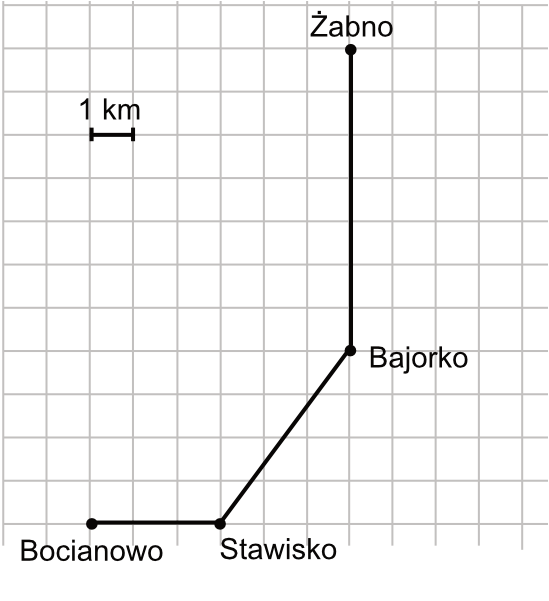
Na kwadratowej siatce Adam przedstawił schemat trasy, którą jechał. O której godzinie Adam dotarł na spotkanie z Bartkiem?

Odpowiedź:      

17:56

Rozwiązanie:      
Krok 1. Obliczenie długości trasy między Stawiskiem i Bajorkiem. Odległość od Stawiska do Bajorka jest przeciwprostokątną trójkąta prostokątnego, którego dolna przyprostokątna ma długość \(3\) kratek, a boczna przyprostokątna ma długość \(4\) kratek: Korzystając z Twierdzenia Pitagorasa możemy zapisać, że w takim razie: $$3^2+4^2=c^2 \           ,\ 9+16=c^2 \           ,\ c^2=25 \           ,\ c=5 \quad\lor\quad c=-5$$ Ujemny wynik odrzucamy, zatem zostaje nam \(c=5\). To oznacza, że trasa od Stawiska do Bajorka ma \(5km\). Krok 2. Obliczenie długości całej trasy. Licząc po kratkach możemy powiedzieć, że: od Bociankowa do Stawiska są \(3km\) od Stawiska do Bajorska jest \(5km\) (to policzyliśmy w pierwszym kroku) od Bajorka do Żabna jest \(7km\) Cała trasa ma więc łącznie długość: $$3km+5km+7km=15km$$ Krok 3. Obliczenie czasu jazdy. Teraz skorzystamy ze wzoru \(v=\frac{s}{t}\), który musimy jeszcze przekształcić: $$v=\frac{s}{t} \           ,\ vt=s \           ,\ t=\frac{s}{v}$$ Wiemy, że \(v=25\frac{km}{h}\), a przed chwilą obliczyliśmy także, że \(s=15km\). Skoro tak, to: $$t=\frac{15km}{25\frac{km}{h}} \           ,\ t=0,6h$$ Musimy jeszcze zamienić ten czas na minuty. Godzina ma \(60\) minut, zatem: $$t=0,6\cdot60min=36min$$ Krok 4. Obliczenie godziny dotarcia na spotkanie. Skoro Adam wyjechał o godzinie 17:20 i jechał \(36\) minut, to do Bartka dotarł o godzinie 17:56.

Teoria:      
W trakcie opracowania