Na rysunku przedstawiony jest wykres funkcji \(f(x)\) określonej dla \(x\in\langle-7;8\rangle\).







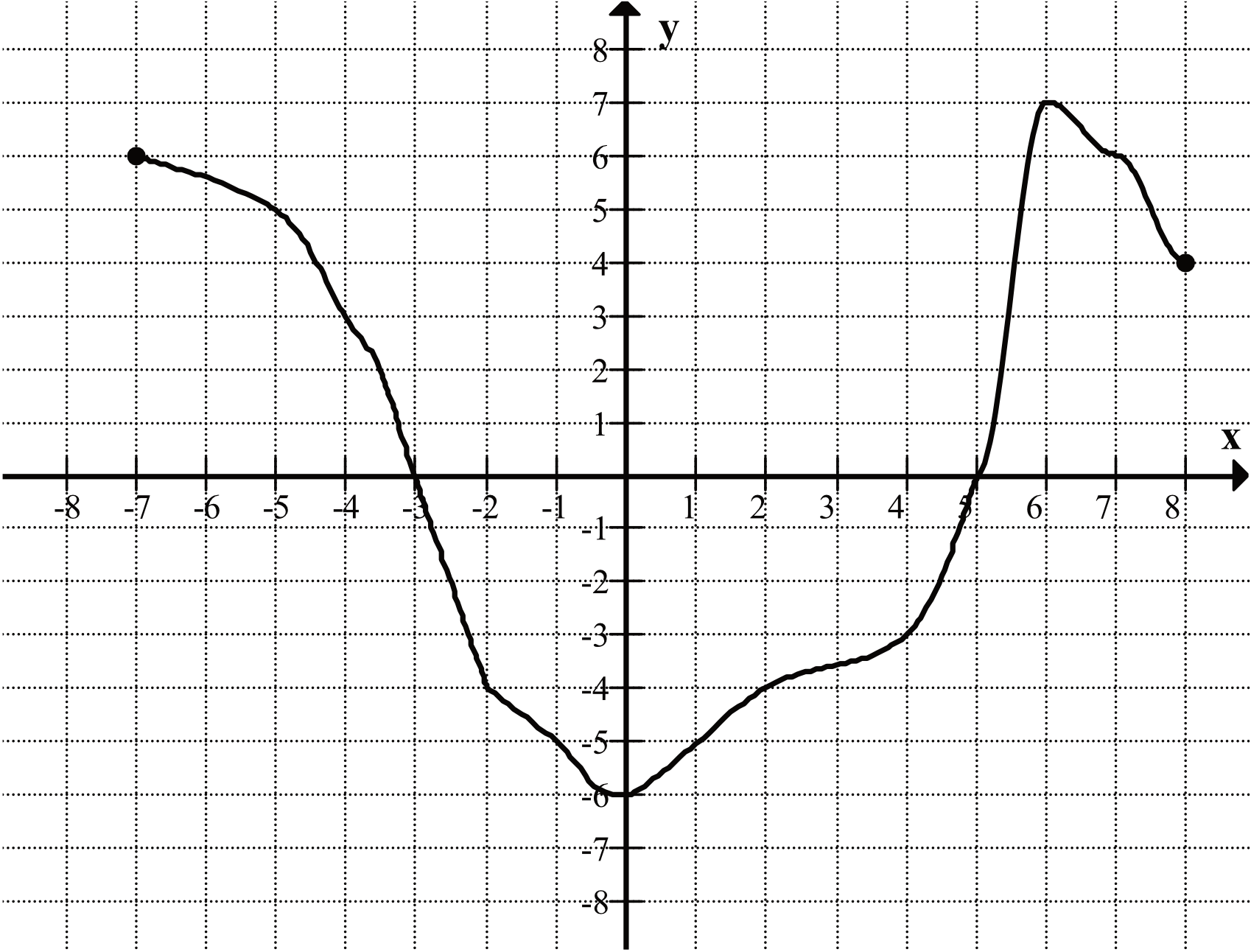
Odczytaj z wykresu i zapisz:

a) największą wartość funkcji \(f\)

b) zbiór rozwiązań nierówności \(f(x)\lt0\)

Odpowiedź:      

a) Największa wartość funkcji to \(y_{max}=7\).
b) \(x\in(-3;5)\)

Rozwiązanie:      
Krok 1. Odczytanie największej wartości funkcji \(f\). Najwyżej położonym punktem na wykresie jest ten o współrzędnych \((6;7)\) w związku z tym największą wartością funkcji jest \(7\). Krok 2. Odczytanie zbioru rozwiązań nierówności \(f(x)\lt0\). Interesuje nas teraz informacja dla jakich argumentów \(x\) funkcja przyjmuje wartości ujemne, czyli tak naprawdę kiedy funkcja znalazła się pod osią \(Ox\). Szukanym zbiorem rozwiązań jest więc \(x\in(-3;5)\).

Teoria:      
W trakcie opracowania