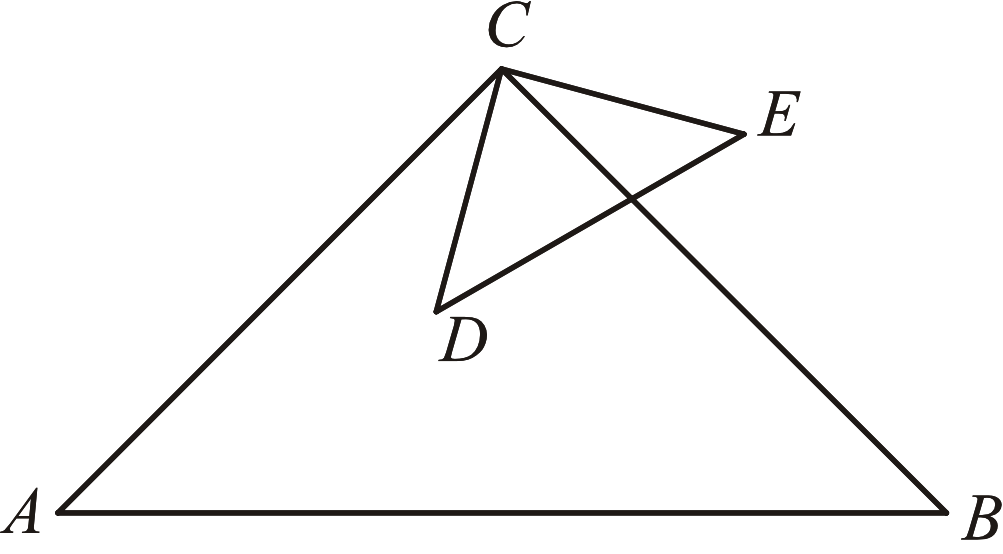
Trójkąty prostokątne równoramienne \(ABC\) i \(CDE\) są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku \(C\) jest prosty). Wykaż, że \(|AD|=|BE|\).

Odpowiedź:      

Udowodniono, że \(|AD|=|BE|\) za pomocą trójkątów przystających (cecha bok-kąt-bok).

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Naszkicujmy rysunek pomocniczy, na którym zaznaczymy wymagane odcinki \(AD\) oraz \(BE\) (patrz kolor niebieski). Krok 2. Udowodnienie, że trójkąty \(ACD\) i \(BCE\) są przystające (cecha bok-kąt-bok). Z treści zadania wynika, że \(|AC|=|BC|\) (patrz: kolor zielony) oraz \(|DC|=|EC|\) (patrz: kolor pomarańczowy). Jeśli jeszcze wykażemy, że trójkąty \(ACD\) i \(BCE\) mają identyczną miarę kąta przy wierzchołku \(C\), to będziemy mogli stwierdzić, że trójkąty \(ACD\) i \(BCE\) są przystające. Jeśli tak rzeczywiście będzie, to będzie to oznaczało, że i trzecia para boków jest równej długości, czyli że \(|AD|=|BE|\). Zaznaczmy sobie na rysunku miary poszczególnych kątów. Z zadania możemy wyczytać, że \(\sphericalangle ACB=90°\) oraz \(\sphericalangle DCE=90°\), a więc: $$α=90°-β \           ,\ γ=90°-β$$ Wykazując, że kąty \(α\) oraz \(γ\) są równej miary zakończyliśmy dowodzenie, bo już wiemy, że trójkąty \(ACD\) i \(BCE\) są przystające na mocy cechy bok-kąt-bok, a więc \(|AD|=|BE|\).

Teoria:      
W trakcie opracowania