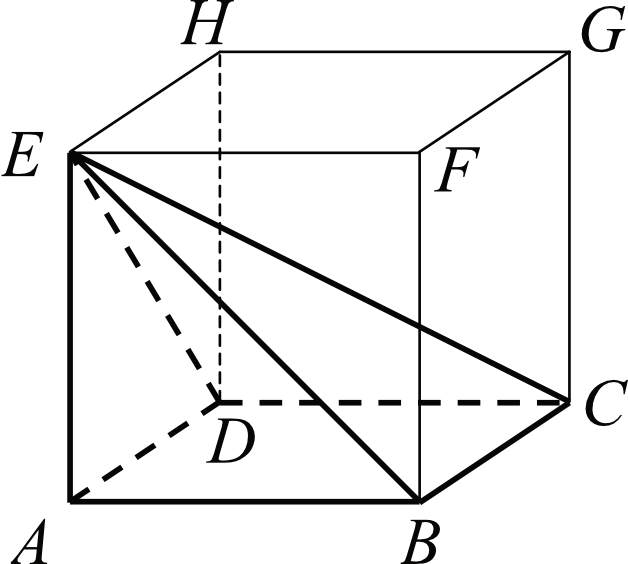
Dany jest sześcian \(ABCDEFGH\). Siatką ostrosłupa czworokątnego \(ABCDE\) jest:

A
B
C
D

Odpowiedź:      

A

Rozwiązanie:      
Zastanówmy się jakie trójkąty znajdą się w naszej siatce ostrosłupa. Trójkąty \(ABE\) oraz \(ADE\) to trójkąty prostokątne równoramienne (wynika to z tego, że odcinki \(AE, AB, AD\) mają jednakową długość, równą długości krawędzi sześcianu). Oprócz tego mamy jeszcze dwa trójkąty \(BCE\) oraz \(CDE\), które także będą prostokątne, ale nie będą już równoramienne (będą tak jakby wydłużone). Po tej prostej analizie możemy odrzucić odpowiedzi \(C\) oraz \(D\), bo tam wszystkie trójkąty mają jednakowe rozmiary. Teraz musimy zastanowić się, która siatka - \(A\) czy \(B\) jest tą poszukiwaną. Te dwie siatki różni tylko ułożenie "dłuższych" trójkątów. W siatce \(A\) przeciwprostokątne dłuższych trójkątów wychodzą z jednego wierzchołka, zatem składając siatkę te długości się na siebie nałożą i to jest to, co nas interesuje. Siatka \(B\) nie złoży się poprawnie, bo ma właśnie źle ułożone te dłuższe trójkąty (dłuższe przeciwprostokątne nie zetkną się). To oznacza, że poprawną siatką jest ta z pierwszej odpowiedzi.

Teoria:      
W trakcie opracowania