Oto wyniki krótkiego sprawdzianu przeprowadzonego w trzech oddziałach II klasy gimnazjum:





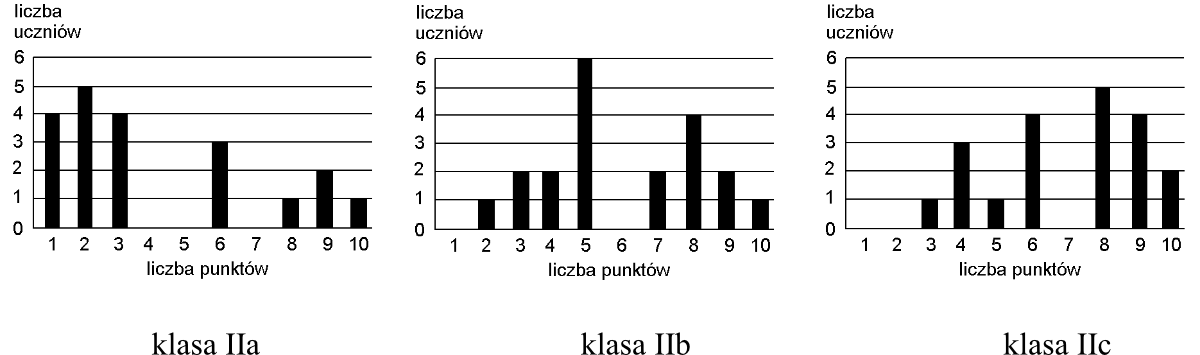
Z porównania wykresów wynika, że sprawdzian był:

A najtrudniejszy dla uczniów z IIa
B najtrudniejszy dla uczniów z IIb
C najtrudniejszy dla uczniów z IIc
D jednakowo trudny dla uczniów z oddziałów a, b i c

Odpowiedź:      

A

Rozwiązanie:      
Generalnie zadanie polega na tym by przeanalizować sobie mniej więcej jak wyglądają te wykresy, bo już po szybkiej analizie możemy określić w której klasie sprawdzian poszedł najgorzej. Zauważmy, że w klasie IIa tylko czterech uczniów zdobyło \(8\) punktów lub więcej. W pozostałych klasach liczba takich uczniów jest znacznie większa (\(7\) osób w klasie IIb oraz \(11\) osób w klasie IIc). Jednocześnie w klasie IIa mamy zdecydowanie najwięcej uczniów, którzy uzyskali bardzo niską punktację \(3\) punkty lub mniej. Takich osób jest aż \(13\). W klasie IIb uczniów mających maksymalnie \(3\) punkty jest tylko trzech, a w klasie IIc jest wręcz tylko jedna taka osoba. To oznacza, że bez cienia wątpliwości możemy stwierdzić, że sprawdzian był najtrudniejszy dla uczniów klasy IIa. Oczywiście nic też nie stoi na przeszkodzie by dokonać tu obliczeń, które potwierdzą nasze spostrzeżenia. Aby odpowiedzieć sobie na pytanie dla której klasy ten sprawdzian był najtrudniejszy musimy wyliczyć średnią liczbę uzyskanych punktów dla każdej z klas. Aby to zrobić musimy obliczyć jaka jest liczba uczniów w każdej klasie i ile łącznie punktów oni zdobyli. Liczbę uczniów obliczymy dodając uczniów którzy zdobyli poszczególną liczbę punktów, natomiast łączną liczbę punktów obliczymy mnożąc ilość zdobytych punktów przez uczniów którzy osiągnęli dany wynik. Klasa IIa: Liczba uczniów: \(4+5+4+3+1+2+1=20\) Liczba łącznie zdobytych punktów: $$4\cdot1+5\cdot2+4\cdot3+3\cdot6+1\cdot8+2\cdot9+1\cdot10= \           ,\ =4+10+12+18+8+18+10=80$$ Średnia zdobytych punktów: \(\frac{80}{20}=4\) Klasa IIb: Liczba uczniów: \(1+2+2+6+2+4+2+1=20\) Liczba łącznie zdobytych punktów: $$1\cdot2+2\cdot3+2\cdot4+6\cdot5+2\cdot7+4\cdot8+2\cdot9+1\cdot10= \           ,\ 2+6+8+30+14+32+18+10=120$$ Średnia zdobytych punktów: \(\frac{120}{20}=6\) Klasa IIc: Liczba uczniów: \(1+3+1+4+5+4+2=20\) Liczba łącznie zdobytych punktów: $$1\cdot3+3\cdot4+1\cdot5+4\cdot6+5\cdot8+4\cdot9+2\cdot10= \           ,\ 3+12+5+24+40+36+20=140$$ Średnia zdobytych punktów: \(\frac{140}{20}=7\)

Teoria:      
W trakcie opracowania