Diagram kołowy przedstawia wyniki wyborów do samorządu szkolnego.





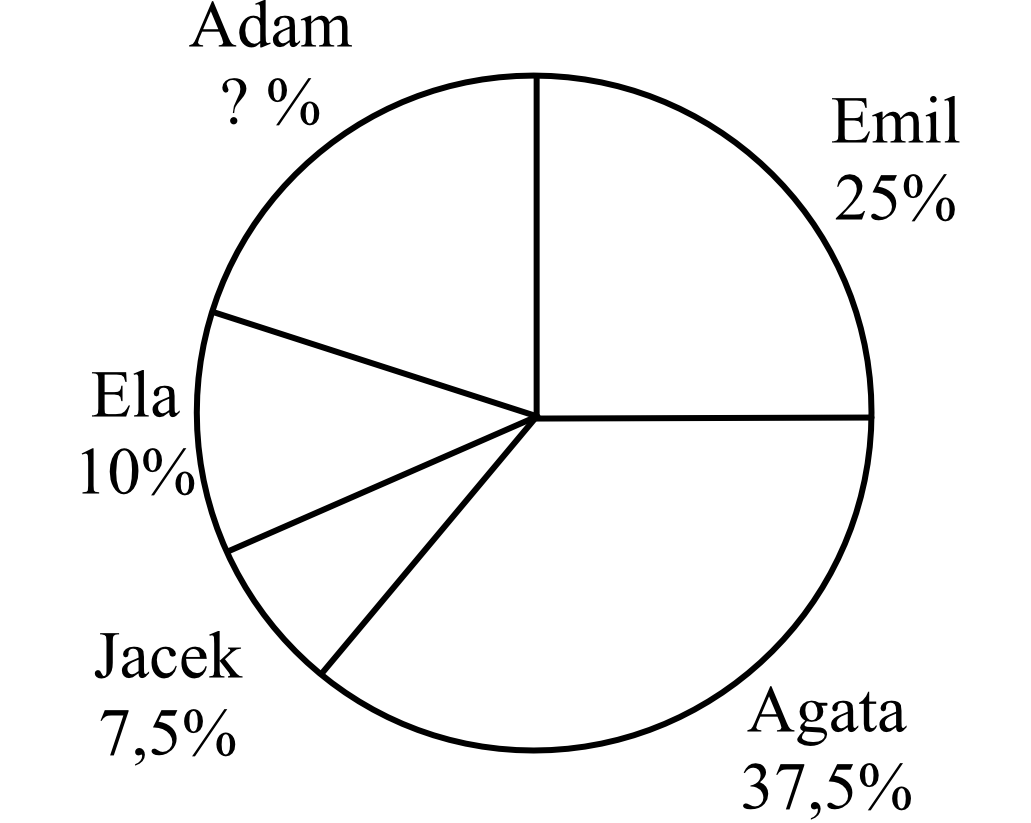
Jaka część uczniów głosowała na Agatę?

A Mniej niż \(\frac{1}{4}\) ogółu
B Mniej niż \(\frac{1}{3}\), ale więcej niż \(\frac{1}{4}\) ogółu
C Więcej niż \(\frac{1}{3}\), ale mniej niż \(\frac{2}{5}\) ogółu
D Więcej niż \(\frac{2}{5}\) ogółu

Odpowiedź:      

C

Rozwiązanie:      
Zadanie można rozwiązać w zasadzie na dwa sposoby: I sposób - zamieniając procenty na ułamki zwykłe. Na Agatę zagłosowało \(37,5\%\) osób. Możemy ten procent zamienić na ułamek zwykły, otrzymując: $$37,5\%=\frac{37,5}{100}=\frac{375}{1000}=\frac{3}{8}$$ Teraz musimy przyrównać otrzymany ułamek do odpowiedzi z treści zadania. Ułamek \(\frac{3}{8}\) jest większy od \(\frac{1}{3}\), bo \(\frac{1}{3}=\frac{3}{9}\) (jeżeli oba ułamki mają ten sam licznik to większy jest ten, który ma mniejszy mianownik). Jednocześnie ułamek \(\frac{3}{8}\) jest mniejszy od \(\frac{2}{5}\). Aby to udowodnić wystarczy sprowadzić obydwa ułamki do wspólnego mianownika: $$\frac{3}{8}=\frac{15}{40} \           ,\ \frac{2}{5}=\frac{16}{40}$$ Z dwóch ułamków mających ten sam mianownik większy jest ten, który ma większy licznik, zatem prawidłowa byłaby odpowiedź trzecia. II sposób - zamieniając ułamki zwykłe na procenty. Ten sposób wydaje się być nieco łatwiejszy w tym przypadku. Tak naprawdę wystarczyłoby pozamieniać ułamki znajdujące się w odpowiedziach na procenty i sprawdzić w którym przedziale znajdzie się nasz ułamek \(37,5\%\). Zamieniając ułamki zwykłe z odpowiedzi na procenty otrzymamy następujące warianty: Odp. A. Mniej niż \(25\%\) ogółu Odp. B. Mniej niż \(33\frac{1}{3}\%\), ale więcej niż \(25\%\) ogółu Odp. C. Więcej niż \(33\frac{1}{3}\%\), ale mniej niż \(40\%\) ogółu Odp. D. Więcej niż \(40\%\) ogółu Widzimy wyraźnie, że \(37,5\%\) mieści się jedynie w przedziale z trzeciej odpowiedzi.

Teoria:      
W trakcie opracowania