Ewa narysowała kwadrat o boku \(1\), prostokąt o bokach \(2\) i \(1\) oraz kąt prosty o wierzchołku \(O\).





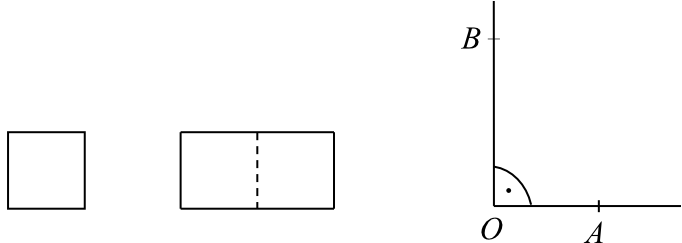
Następnie od wierzchołka \(O\) kąta prostego odmierzyła na jednym ramieniu kąta odcinek \(OA\) o długości równej przekątnej kwadratu, a na drugim ramieniu - odcinek \(OB\) o długości równej przekątnej prostokąta. Długość odcinka \(AB\) jest równa:

A \(\sqrt{7}\)
B \(\sqrt{2}+\sqrt{5}\)
C \(\sqrt{5}\)
D \(\sqrt{2}+\sqrt{3}\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Obliczenie długości odcinka \(OA\). Odcinek \(OA\) jest przekątną kwadratu o boku \(1\). Wiedząc, że przekątna kwadratu o boku \(a\) ma długość \(a\sqrt{2}\) możemy zapisać, że odcinek \(OA\) ma miarę: $$|OA|=1\cdot\sqrt{2}=\sqrt{2}$$ Krok 2. Obliczenie długości odcinka \(OB\). Długość odcinka \(OB\) jest przekątną prostokąta o bokach \(2\) i \(1\). Możemy więc do wyznaczenia długości przekątnej skorzystać z Twierdzenia Pitagorasa: $$1^2+2^2=c^2 \           ,\ 1+4=c^2 \           ,\ c^2=5 \           ,\ c=\sqrt{5}$$ Zatem \(|OB|=\sqrt{5}\). Krok 3. Obliczenie długości odcinka \(AB\). Tutaj ponownie skorzystamy z Twierdzenia Pitagorasa. Krótsza przyprostokątna \(OA=\sqrt{2}\), dłuższa przyprostokątna \(|OB|=\sqrt{5}\), więc przeciwprostokątna \(AB\) będzie równa: $$(\sqrt{2})^2+(\sqrt{5})^2=c^2 \           ,\ 2+5=c^2 \           ,\ c^2=7 \           ,\ c=\sqrt{7}$$ To oznacza, że długość odcinka \(AB\) jest równa \(\sqrt{7}\).

Teoria:      
W trakcie opracowania