W układzie współrzędnych narysowano sześciokąt foremny o boku \(2\) tak, że jednym z jego wierzchołków jest punkt \((0,0)\), a jeden z jego boków leży na osi \(x\) (rysunek).





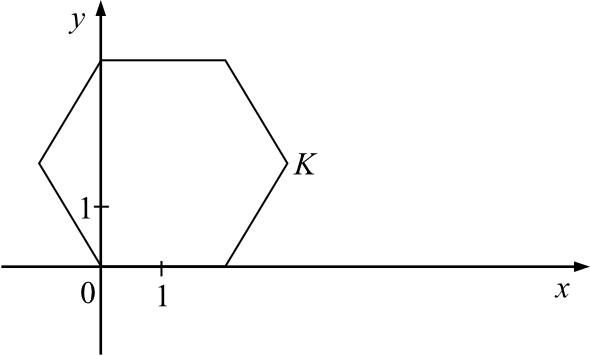
Współrzędne wierzchołka \(K\) tego sześciokąta są równe:

A \((3, \sqrt{3})\)
B \((\sqrt{3}, 3)\)
C \((\sqrt{3}, \frac{\sqrt{3}}{2})\)
D \((3, \frac{\sqrt{3}}{2})\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. W sześciokącie foremnym wszystkie kąty wewnętrzne mają miarę \(120°\). Wykorzystując własności kątów możemy sobie narysować następujący szkic: Wiemy, że kąt \(BAK\) ma miarę \(60°\), bo jest to kąt przyległy do kąta \(120°\), a suma miar kątów przyległych jest równa \(180°\). To z kolei oznacza, że powstał nam klasyczny trójkąt o mierze kątów \(30°, 60°, 90°\) z którego własności musimy teraz skorzystać. Krok 2. Wyznaczenie długości odcinków \(AB\) oraz \(BK\). Zgodnie z własnościami trójkątów \(30°, 60°, 90°\) możemy zapisać, że długość odcinka \(AB\) jest dwa razy krótsza od długości przeciwprostokątnej, czyli: $$|AB|=2:2=1$$ Dłuższa przyprostokątna jest o \(\sqrt{3}\) razy większa od krótszej przyprostokątnej, zatem: $$|BK|=a\sqrt{3}=1\cdot\sqrt{3}=\sqrt{3}$$ Krok 3. Zapisanie współrzędnych punktu \(K\). Współrzędną iksową stanowi suma długości boku sześcianu oraz długości dolnej podstawy trójkąta, zatem: $$x=2+1=3$$ Współrzędna iksowa jest równa długości odcinka \(BK\), zatem: $$y=\sqrt{3}$$ To oznacza, że współrzędne punktu \(K\) są następujące: $$K=(3;\sqrt{3})$$

Teoria:      
W trakcie opracowania