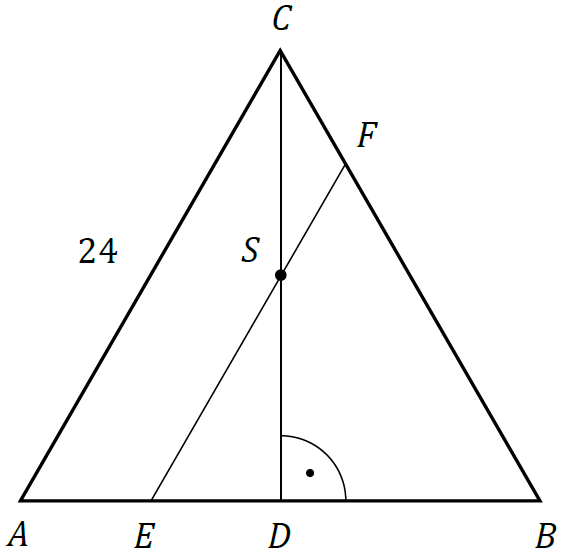
Dany jest trójkąt równoboczny \(ABC\) o boku długości \(24\). Punkt \(E\) leży na boku \(AB\), a punkt \(F\) - na boku \(BC\) tego trójkąta. Odcinek \(EF\) jest równoległy do boku \(AC\) i przechodzi przez środek \(S\) wysokości \(CD\) trójkąta \(ABC\) (zobacz rysunek). Oblicz długość odcinka \(EF\).

Odpowiedź:      

\(|EF|=18\)

Rozwiązanie:      
Krok 1. Obliczenie wysokości trójkąta \(ABC\). Trójkąt \(ABC\) jest równoboczny o boku długości \(a=24\). Korzystając ze wzoru na wysokość takiego trójkąta, wyjdzie nam, że: $$h=\frac{a\sqrt{3}}{2} \           ,\ h=\frac{24\sqrt{3}}{2} \           ,\ h=12\sqrt{3}$$ Tym samym możemy zapisać, że \(|CD|=12\sqrt{3}\). Krok 2. Obliczenie długości odcinka \(DS\) oraz \(AD\). Środek wysokości \(S\) dzieli wysokość \(CD\) na dwie równe części, zatem długość odcinka \(DS\) będzie równa: $$|DS|=12\sqrt{3}:2 \           ,\ |DS|=6\sqrt{3}$$ Dodatkowo możemy od razu policzyć długość odcinka \(AD\). W trójkątach równobocznych wysokość dzieli podstawę na dwie równe części, zatem: $$|AD|=24:2 \           ,\ |AD|=12$$ Krok 3. Dostrzeżenie podobieństwa trójkątów i ułożenie odpowiedniego równania. Skoro odcinek \(EF\) jest równoległy do boku \(AC\), to trójkąty \(ADC\) oraz \(EDS\) są trójkątami podobnymi. Możemy więc zapisać, że: $$\frac{|CD|}{|AD|}=\frac{|DS|}{|ED|} \           ,\ \frac{12\sqrt{3}}{12}=\frac{6\sqrt{3}}{|ED|}$$ Mnożąc na krzyż, otrzymamy: $$12\sqrt{3}\cdot|ED|=12\cdot6\sqrt{3} \           ,\ |ED|=6$$ Ewentualnie można do tematu podejść jeszcze inaczej, korzystając ze skali podobieństwa. Spójrzmy na trójkąty prostokątne \(ADC\) oraz \(EDS\). Są to trójkąty podobne w skali podobieństwa \(k=\frac{1}{2}\) (bo wysokość \(SD\) jest dwa razy mniejsza od wysokości \(CD\)). Skoro tak, to dolna przyprostokątna \(ED\) jest dwa razy krótsza od przyprostokątnej \(AD\), więc: $$|ED|=k\cdot|AD| \           ,\ |ED|=\frac{1}{2}\cdot12=6$$ Krok 4. Obliczenie długości odcinka \(EF\). Spójrzmy na trójkąt \(EBF\). Jest on trójkątem podobnym do trójkąta \(ABC\), a więc też jest on równoboczny. Z dotychczasowych obliczeń wynika, że \(|ED|=6\) oraz \(|DB|=12\), a więc \(|EB|=6+12=18\). To oznacza, że długość wszystkich boków tego trójkąta ma długość \(18\), czyli tym samym \(|EF|=18\).

Teoria:      
W trakcie opracowania