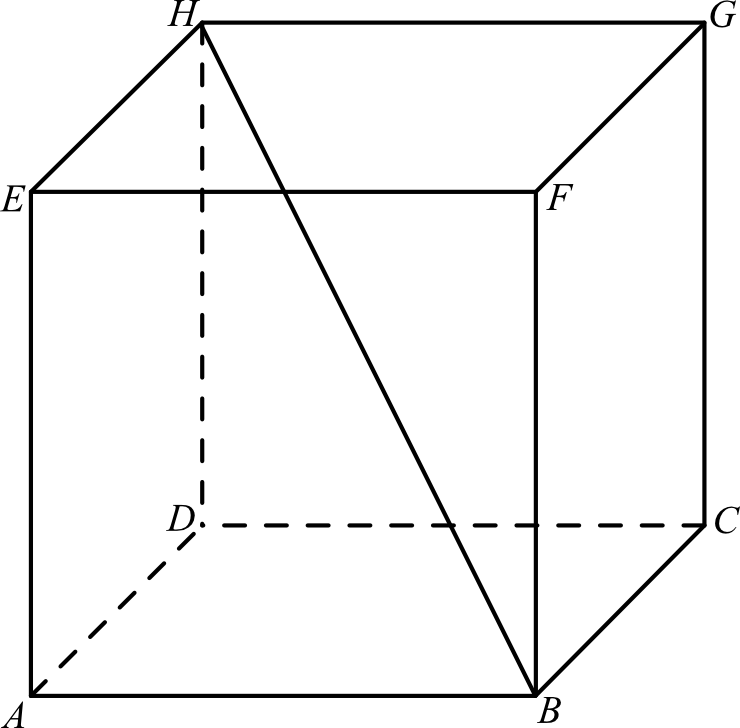
Podstawą graniastosłupa \(ABCDEFGH\) jest prostokąt \(ABCD\) (zobacz rysunek), którego krótszy bok ma długość \(3\). Przekątna prostokąta \(ABCD\) tworzy z jego dłuższym bokiem kąt \(30°\). Przekątna \(HB\) graniastosłupa tworzy z płaszczyzną jego podstawy kąt \(60°\). Oblicz objętość tego graniastosłupa.

Odpowiedź:      

\(V=162\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Zaznaczmy sobie na rysunku kąty \(30°\) i \(60°\) oraz odpowiednie długości boków omówione w treści zadania: Wbrew pozorom już podczas zaznaczania odpowiednich długości można było popełnić spory błąd. Skąd wiemy, że to akurat boki \(AD\) oraz analogicznie \(BC\) są tymi krótszymi i akurat one mają długość \(3\)? Treść zadania nie sugeruje nam tego wprost, ale wynika to chociażby z własności trójkątów \(30°\), \(60°\), \(90°\), a takim jest trójkąt \(ABD\). W takich trójkątach dłuższą przyprostokątną jest ten bok, który znajduje się przy kącie \(30°\) i stąd też wiemy, że dłuższymi krawędziami są \(AB\) oraz analogicznie \(CD\), a krótszymi są \(AD\) oraz \(BC\). Do obliczenia objętości będziemy potrzebowali znać długości boków prostokąta oraz wysokość całego graniastosłupa, zatem wyznaczmy po kolei każdą z wartości. Krok 2. Obliczenie miary dłuższego boku prostokąta. Do obliczenia długości, którą oznaczyliśmy sobie jako \(a\) skorzystamy z trójkąta \(ABD\). Użyjemy tutaj albo własności trójkąta \(30°, 60°, 90°\), albo funkcji tangensa: $$tg30°=\frac{3}{a} \           ,\ \frac{\sqrt{3}}{3}=\frac{3}{a}$$ Mnożąc na krzyż otrzymamy: $$\sqrt{3}a=9 \           ,\ a=\frac{9}{\sqrt{3}}=\frac{9\cdot\sqrt{3}}{\sqrt{3}\cdot\sqrt{3}}=\frac{9\sqrt{3}}{3}=3\sqrt{3}$$ Krok 3. Obliczenie długości przekątnej podstawy. Ponownie spoglądamy na trójkąt \(ABD\). Do obliczenia długości przekątnej \(DB\) skorzystamy z Twierdzenia Pitagorasa i z miary boku prostokąta, którą obliczyliśmy przed chwilą: $$3^2+(3\sqrt{3})^2=|DB|^2 \           ,\ 9+9\cdot3=|DB|^2 \           ,\ 9+27=|DB|^2 \           ,\ |DB|^2=36 \           ,\ |DB|=6$$ Krok 4. Obliczenie wysokości graniastosłupa. Tym razem interesuje nas trójkąt \(DBH\). Odcinek \(DH\), który oznaczyliśmy sobie jako \(H\) wyliczymy z funkcji tangensa (właśnie po to liczyliśmy przed chwilą długość przekątnej \(DB\)): $$tg60°=\frac{H}{6} \           ,\ \sqrt{3}=\frac{H}{6} \           ,\ H=6\sqrt{3}$$ Krok 5. Obliczenie objętości graniastosłupa. Znamy wszystkie potrzebne miary, więc możemy przejść do obliczeń objętości: $$V=P_{p}\cdot H \           ,\ V=3\cdot3\sqrt{3}\cdot6\sqrt{3} \           ,\ V=9\sqrt{3}\cdot6\sqrt{3} \           ,\ V=54\cdot3 \           ,\ V=162$$

Teoria:      
W trakcie opracowania