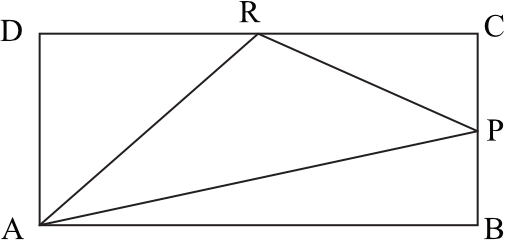
W prostokącie \(ABCD\) punkt \(P\) jest środkiem boku \(BC\), a punkt \(R\) jest środkiem boku \(CD\). Wykaż, że pole trójkąta \(APR\) jest równe sumie pól trójkątów \(ADR\) oraz \(PCR\).

Odpowiedź:      

Udowodniono obliczając miary pól poszczególnych trójkątów.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku poglądowego. Oznaczmy sobie na rysunku poszczególne długości odcinków: Krok 2. Obliczenie pól trójkątów \(ADR\), \(PCR\) oraz \(ABP\), a także prostokąta \(ABCD\). $$P_{ADR}=\frac{1}{2}\cdot\frac{1}{2}a\cdot b=\frac{1}{4}ab \           ,\ P_{PCR}=\frac{1}{2}\cdot\frac{1}{2}a\cdot\frac{1}{2}b=\frac{1}{8}ab \           ,\ P_{ABP}=\frac{1}{2}\cdot a\cdot\frac{1}{2}b=\frac{1}{4}ab \           ,\ P_{ABCD}=ab$$ Krok 3. Obliczenie pola trójkąta \(APR\). Pole trójkąta \(APR\) obliczymy odejmując od pola prostokąta pola trzech trójkątów, zatem: $$P_{APR}=P_{ABCD}-P_{ADR}-P_{PCR}-P_{ABP} \           ,\ P_{APR}=ab-\frac{1}{4}ab-\frac{1}{8}ab-\frac{1}{4}ab \           ,\ P_{APR}=ab-\frac{2}{8}ab-\frac{1}{8}ab-\frac{2}{8}ab \           ,\ P_{APR}=ab-\frac{5}{8}ab \           ,\ P_{APR}=\frac{3}{8}ab$$ Krok 4. Zakończenie dowodzenia. Suma pól trójkątów \(ADR\) oraz \(PCR\) jest równa: $$P_{ADR}+P_{PCR}=\frac{1}{4}ab+\frac{1}{8}ab=\frac{3}{8}ab$$ Otrzymany wynik jest dokładnie taki sam jak wyznaczone pole trójkąta \(APR\) w trzecim kroku, a to kończy nasz dowód.

Teoria:      
W trakcie opracowania