Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura poprawkowa z matematyki (poziom podstawowy) - Sierpień 2017 Zadanie 21 z 34
Zadanie nr 21. (1pkt)
Prosta \(l\) jest nachylona do osi \(Ox\) pod kątem \(30°\) i przecina oś \(Oy\) w punkcie \((0,-\sqrt{3})\) (zobacz rysunek).
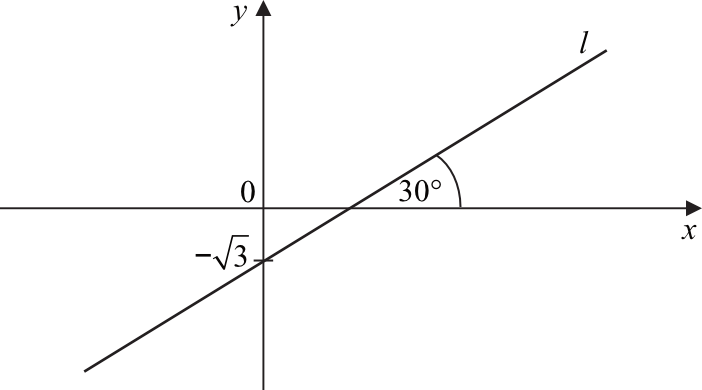
Prosta \(l\) ma równanie:
A \(y=\frac{\sqrt{3}}{3}x-\sqrt{3}\)
B \(y=\frac{\sqrt{3}}{3}x+\sqrt{3}\)
C \(y=\frac{1}{2}x-\sqrt{3}\)
D \(y=\frac{1}{2}x+\sqrt{3}\)
Rozwiązanie:
Krok 1. Ustalenie wartości współczynnika kierunkowego \(a\).
Nasza prosta będzie wyrażać się wzorem \(y=ax+b\). Musimy teraz ustalić jakie są wartości współczynników \(a\) oraz \(b\). Współczynnik kierunkowy \(a\) jest równy tangensowi kąta nachylenia tej prostej do osi iksów. W związku z tym:
$$a=tg30° \ ,\
a=\frac{\sqrt{3}}{3}$$
Krok 2. Ustalenie wartości współczynnika \(b\).
Współczynnik \(b\) mówi nam o tym w którym miejscu prosta przecina się z osią igreków. Widzimy, że prosta przecina oś igreków dla \(y=-\sqrt{3}\), zatem \(b=-\sqrt{3}\).
To oznacza, że prosta \(l\) wyrażona jest równaniem \(y=\frac{\sqrt{3}}{3}x-\sqrt{3}\).
Teoria:
W trakcie opracowania
matura poprawkowa - CKE

