Zbiory arkuszy maturalnych z matematyki. Nasza strona oferuje bogaty wybór przykładowych arkuszy, rozwiązań zadań, testów z matematyki oraz wiele innych materiałów
Matura próbna z matematyki (poziom podstawowy) - Listopad 2010 Zadanie 8 z 34
Zadanie nr 8. (1pkt)
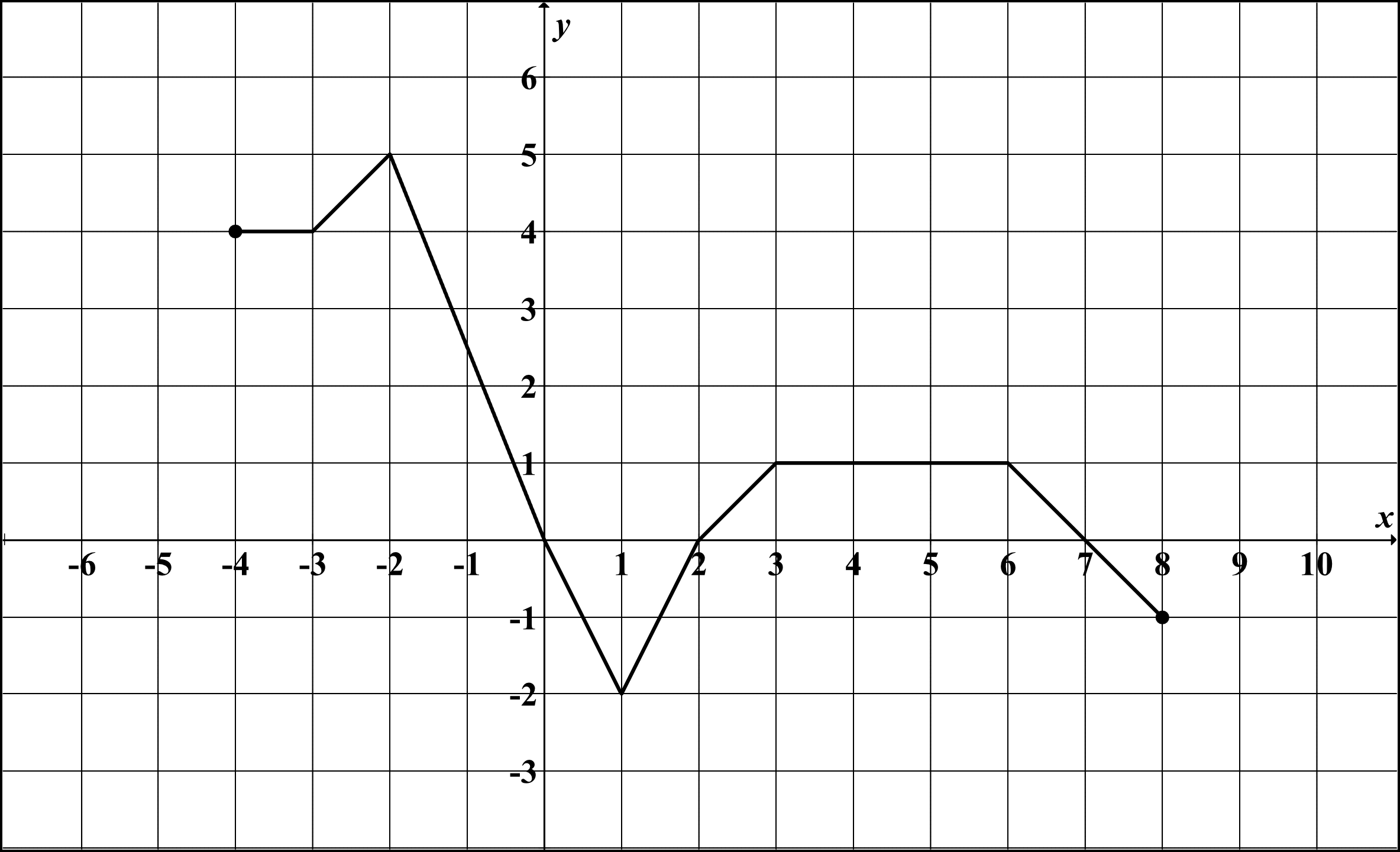
Poniżej przedstawiono wykres funkcji \(f\). Korzystając z tego wykresu, wskaż nierówność prawdziwą.
A \(f(-1)\lt f(1)\)
B \(f(1)\lt f(3)\)
C \(f(-1)\lt f(3)\)
D \(f(3)\lt f(0)\)
Rozwiązanie:
Przykładowo zapis \(f(-1)\) oznacza, że musimy odczytać wartość funkcji dla argumentu \(x=-1\). W naszym przypadku \(f(-1)\) jest równe niespełna \(3\). Musimy sprawdzić tak po kolei każdą z par i zweryfikować która nierówność jest prawdziwa:
Odp. A. \(f(-1)\lt f(1)\)
Komentarz: Ta nierówność jest nieprawdziwa, bo \(f(-1)\) to niespełna \(3\), natomiast \(f(1)=-2\).
Odp. B. \(f(1)\lt f(3)\)
Komentarz: Ta nierówność jest prawdziwa, bo \(f(1)=-2\), natomiast \(f(3)=1\), a więc to \(f(1)\) jest mniejsze od \(f(3)\).
Odp. C. \(f(-1)\lt f(3)\)
Komentarz: Ta nierówność jest nieprawdziwa, bo \(f(-1)\) to niespełna \(3\), natomiast \(f(3)=1\).
Odp. D. \(f(3)\lt f(0)\)
Komentarz: Ta nierówność jest nieprawdziwa, bo \(f(3)=1\), natomiast \(f(1)=-2\).
Teoria:
W trakcie opracowania
matura próbna - CKE

