Pojedynczy znak w piśmie Braille’a dla niewidomych jest kombinacją od \(1\) do \(6\) wypukłych punktów, które mogą zajmować miejsca ułożone w dwóch kolumnach po trzy miejsca w każdej kolumnie. Poniżej podano przykład napisu w piśmie Braille’a. Czarne kropki w znaku oznaczają wypukłości, a białe kropki oznaczają brak wypukłości. Pojedynczy znak w piśmie Braille’a musi zawierać co najmniej jeden punkt wypukły.





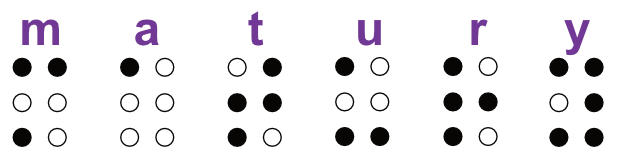
Oblicz, ile różnych pojedynczych znaków można zapisać w piśmie Braille’a.

Odpowiedź:      

\(63\)

Rozwiązanie:      
Każdy punkt może być "zapełniony" na jeden z dwóch sposobów (może być wypukły lub nie). Zgodnie z regułą mnożenia to oznacza, że wszystkich możliwości utworzenia znaku będziemy mieć: $$2\cdot2\cdot2\cdot2\cdot2\cdot2=64$$ Ale to nie koniec. Pod koniec treści zadania mamy uwagę, że każdy znak w piśmie Braille’a musi zawierać co najmniej jeden punkt wypukły. To oznacza, że spośród \(64\) obliczonych możliwości musimy jedną odrzucić (tę, która miałaby wszystkie kropki niewypukłe). Skoro tak, to wszystkich znaków będziemy mieć: $$64-1=63$$

Teoria:      
W trakcie opracowania