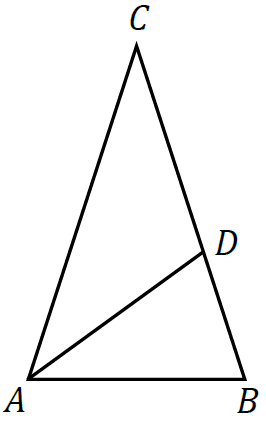
Dany jest trójkąt równoramienny \(ABC\), w którym \(|AC|=|BC|\). Dwusieczna kąta \(BAC\) przecina bok \(BC\) w takim punkcie \(D\), że trójkąty \(ABC\) i \(BDA\) są podobne (zobacz rysunek). Oblicz miarę kąta \(BAC\).

Odpowiedź:      

\(|\sphericalangle BAC|=72°\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Oznaczmy kąt \(BAC\) jako kąt \(\alpha\). Z tego kąta poprowadzono dwusieczną, co prowadzi nas do wniosku, że \(|\sphericalangle DAB|=\frac{1}{2}\alpha\) oraz \(|\sphericalangle CAD|=\frac{1}{2}\alpha\). Warto też zauważyć, że skoro jest to trójkąt równoramienny, to także \(|\sphericalangle ABC|=\alpha\). Sytuacja będzie więc wyglądać następująco: Krok 2. Wyznaczenie miary kąta \(BAC\). Spójrzmy teraz na trójkąt \(ABD\). Jest to trójkąt podobny do trójkąta \(ABC\), czyli także musi być on równoramienny. Kąty przy podstawie takich trójkątów mają jednakową miarę (tutaj jest podstawa \(BD\)), zatem \(|\sphericalangle ADB|=\alpha\). W ten sposób opisaliśmy już symbolami wszystkie kąty w trójkącie \(ABD\). Suma kątów w trójkącie musi być równa \(180°\), zatem: $$\frac{1}{2}\alpha+\alpha+\alpha=180° \           ,\ 2,5\alpha=180° \           ,\ \alpha=72°$$ Zgodnie z oznaczeniami, miara kąta \(\alpha\) jest także miarą poszukiwanego przez nas kąta \(BAC\), zatem: $$|\sphericalangle BAC|=72°$$

Teoria:      
W trakcie opracowania