Podstawy trapezu prostokątnego \(ABCD\) mają długości \(AB=13\), \(CD=11\). Prosta będąca symetralną ramienia \(AD\) przecina to ramię w punkcie \(E\), a ramię \(BC\) - prostopadłe do podstaw trapezu - w punkcie \(F\), takim że \(BF=1\) (jak na rysunku).





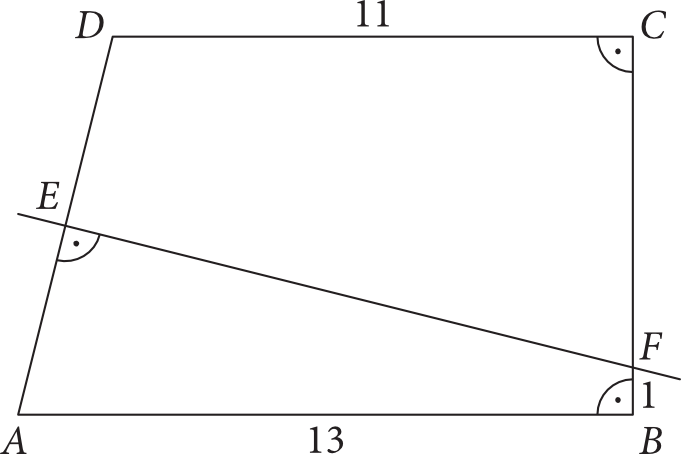
Oblicz pole trapezu \(ABCD\).

Odpowiedź:      

\(P=96\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Skoro punkt \(E\) przecina odcinek \(AD\) w połowie długości, a bok \(EF\) jest prostopadły do boku \(AD\), to łącząc punkty \(A\) z \(F\) oraz \(D\) z \(F\) otrzymamy tak naprawdę trójkąt równoramienny \(AFD\), którego wysokością jest odcinek \(EF\): A skąd wiemy, że jest to trójkąt równoramienny? Możemy być tego pewni, ponieważ wysokość trójkąta dzieli podstawę na dwie równe części, a to charakterystyczny element trójkątów równoramiennych. Krok 2. Obliczenie długości odcinka \(AF\) oraz \(DF\). Spójrzmy na trójkąt prostokątny \(ABF\). To właśnie z tego trójkąta jesteśmy w stanie obliczyć długość odcinka \(AF\), korzystając z Twierdzenia Pitagorasa: $$13^2+1^2=|AF|^2 \           ,\ 169+1=|AF|^2 \           ,\ |AF|^2=170 \           ,\ |AF|=\sqrt{170} \quad\lor\quad |AF|=-\sqrt{170}$$ Ujemny wynik oczywiście odrzucamy, bo długość boku nie może być ujemna. To oznacza, że zarówno \(|AF|=\sqrt{170}\) jak i \(|DF|=\sqrt{170}\). Póki co możemy te wyniki zostawić w takiej postaci. Krok 3. Obliczenie długości odcinka \(CF\). Spójrzmy teraz na trójkąt \(DCF\). Jest to także trójkąt prostokątny, znamy dwie długości boków tego trójkąta, zatem z pomocą po raz kolejny przyjdzie nam Twierdzenie Pitagorasa: $$11^2+|CF|^2=(\sqrt{170})^2 \           ,\ 121+|CF|^2=170 \           ,\ |CF|^2=49 \           ,\ |CF|=7 \quad\lor\quad |CF|=-7$$ Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(|CF|=7\). Krok 4. Obliczenie długości boku \(BC\). Jest to trapez prostokątny, zatem bok \(BC\) będzie jednocześnie wysokością naszej figury. Skoro znamy długości odcinków \(|BF|=1\) oraz \(|CF|=7\), to wyznaczenie długości boku \(BC\) jest formalnością: $$|BC|=|BF|+|CF| \           ,\ |BC|=1+7 \           ,\ |BC|=8$$ Krok 5. Obliczenie pola powierzchni trapezu. Mamy wszystkie potrzebne dane do obliczenia pola trapezu, ponieważ znamy długości obydwu podstaw oraz wysokości. W związku z tym: $$P=\frac{1}{2}(a+b)\cdot h \           ,\ P=\frac{1}{2}(13+11)\cdot8 \           ,\ P=\frac{1}{2}\cdot24\cdot8 \           ,\ P=12\cdot8 \           ,\ P=96$$

Teoria:      
W trakcie opracowania